Math Financeira

35) Exercícios Propostos – Equivalência Financeira em Juros Compostos

Matemática Financeira e suas aplicações

Written by

Ricardo Lacerda

em

, ,

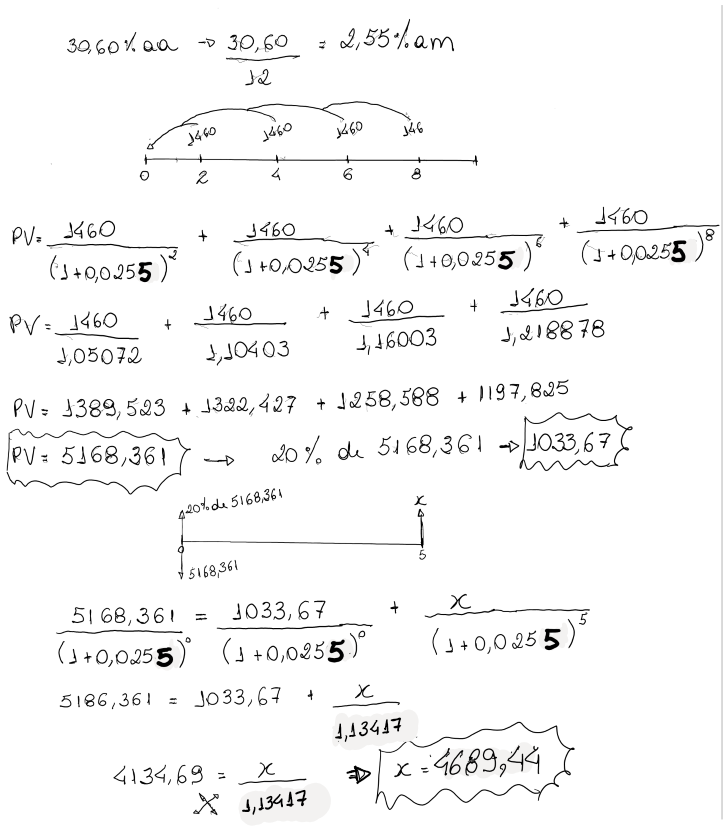
Determinada mercadoria foi adquirida em 4 pagamentos bimestrais de R$1.460,00 cada um. Alternativamente, esta mesma mercadoria poderia ser adquirida pagando-se 20% de seu valor como entrada e o restante ao final de 5 meses. Sendo de 30,60% a.a. a taxa nominal de juros com capitalização mensal a ser considerada nesta operação, pede-se determinar o valor da prestação vencível ao final de 5 meses.

Untitled

Eu te ajudei? Faça uma doação única para ajudar no meu trabalho.

Escolha um valor

R$5,00
R$10,00
R$15,00

Ou insira uma quantia personalizada

R$

Obrigado pela sua contribuição.

Faça uma doação

Comentários

10 respostas a “35) Exercícios Propostos – Equivalência Financeira em Juros Compostos”

  1. Avatar de Ronaldo Oliveira
    Ronaldo Oliveira

    Olá, Ricardo. Mais uma vez, parabéns pelo trabalho dispensado, grato pelo conteúdo. Ao achar o PV = 5.168, 36, eu pensei que a questão pudesse ser resolvida do seguinte modo:

    20% de PV = 1033, 67, sendo assim, o PV a ser financiado, o qual constituirá a parcela, 5.168, 36 – 1033,67, ou seja, 4.134,69. Em conclusão, aplicaria a fórmula:

    PF=PV(1+I)^n

    O resultado dá diferente do aplicado na questão. Poderia me dizer o que há de errado no meu procedimento?

    Curtir

    Responder
    1. Avatar de Ricardo Lacerda
      Ricardo Lacerda

      Ronaldo
      A sua dúvida me ajudou a identificar um erro na solução do exercício e também no resultado apresentado no gabarito no livro.
      O seu raciocínio está correto.

      VF = valor futuro (prestação ao final do período)
      PV = valor presente (valor financiado), que é R$ 4.134,69
      i = taxa de juros mensal = 0,0255
      n = número de meses = 5

      Agora, substituindo os valores na fórmula:
      VF=4134,69×(1+0,0255) ^ 5
      VF=4.134,69×(1,0255) ^ 5

      Calculando (1+0,0255) ^ 5 = 1,13417
      VF=4.134,69×1,13417 = R$4689,44

      O valor da prestação vencível ao final de 5 meses, com precisão, é R$ 4.689,44

      Este é o valor correto para o problema mencionado.

      Curtir

      Responder
  2. Avatar de Jemmys
    Jemmys

    Oi, tudo bem? Primeiramente, grato por disponibilizar as resoluções, estão ajudando muito. Uma pergunta, você tem as resoluções de todos os exercícios do livro? Notei que suas resoluções sõ melhores do que aquelas apresentadas no livro.

    Curtido por 1 pessoa

    Responder
    1. Avatar de Ricardo Lacerda
      Ricardo Lacerda

      Eu tenho as resoluções das questões que resolvi e que estão publicadas. Eu fechei todos os exercícios dos assuntos que estão disponíveis no menu.
      Obrigado pela visita

      Curtir

      Responder
  3. Avatar de gustavo
    gustavo

    pq vc dividiu a taxa de juros por 12 e não fez a formula da taxa efetiva?

    Curtir

    Responder
    1. Avatar de Ricardo Lacerda
      Ricardo Lacerda

      Porque foi informado que 30,60% era uma taxa nominal anual. Sendo uma taxa nominal de juros podemos dividir que teremos uma taxa nominal mensal para o período.

      Curtir

      Responder
  4. Avatar de julio
    julio

    Por que você multiplicou por 1,02505 sendo que é 2,55% a.m. ?

    Curtir

    Responder
    1. Avatar de Ricardo Lacerda
      Ricardo Lacerda

      2,55% = 2,55/100 = (0,0255 +1 )

      A fórmula no denominador corresponde a :

      (1+ i) elevado a n

      Curtir

      Responder
      1. Avatar de Sandra Lima
        Sandra Lima

        Mas 2,55/100 dá 0,0255 e não 0,02505. Então 0,255 + 1dá 1,0255 e não 1,02505.

        Curtido por 1 pessoa

      2. Avatar de Ricardo Lacerda
        Ricardo Lacerda

        Obrigado pela observação. Vou providenciar a correção na questão.

        Curtido por 1 pessoa

Deixar mensagem para julio Cancelar resposta

More posts