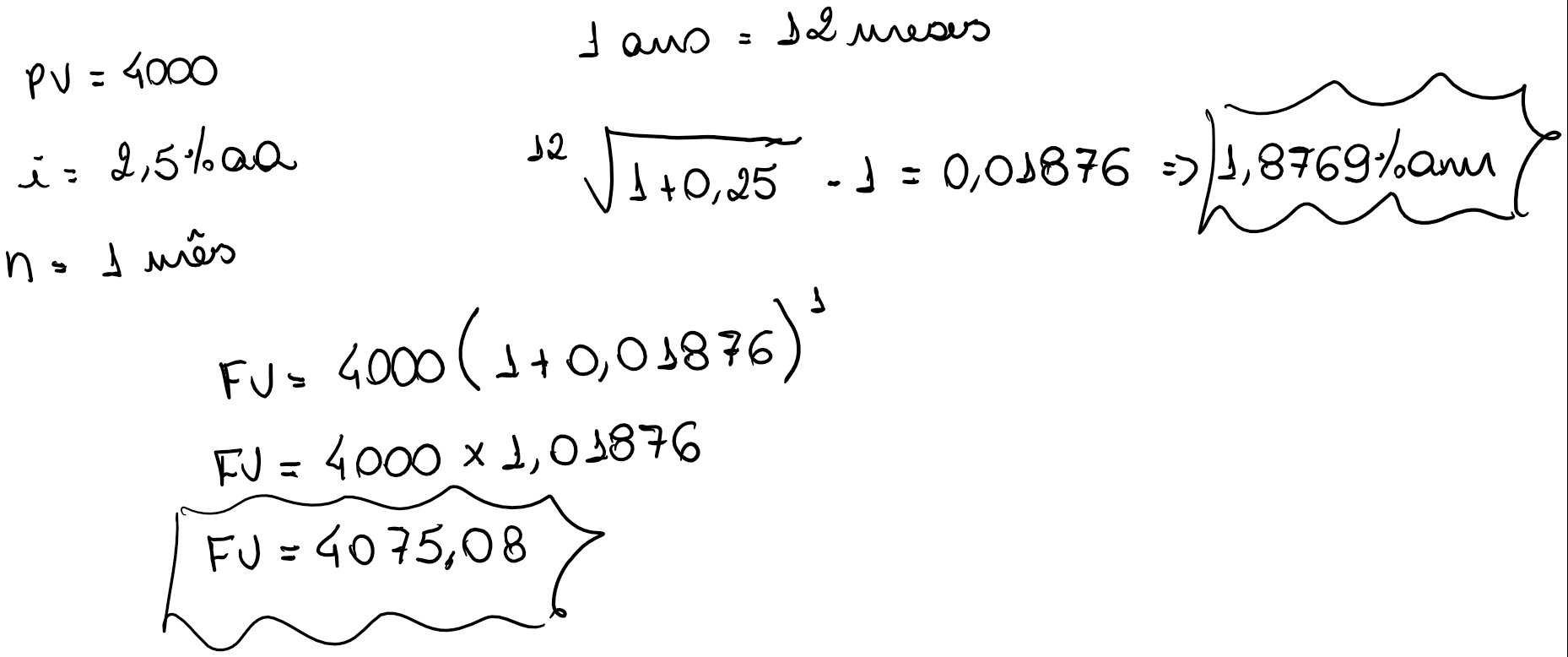
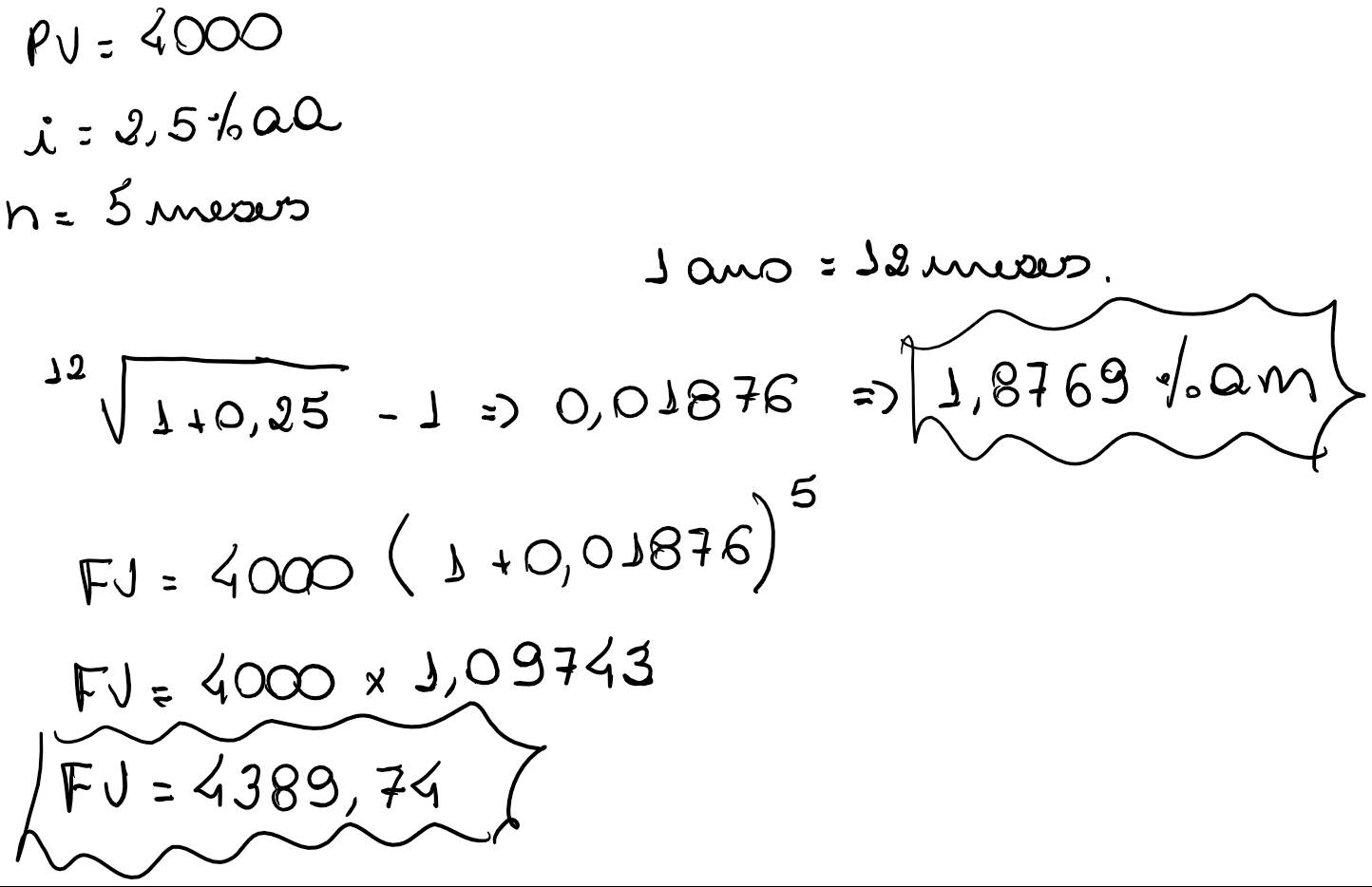
Escolha um valor
Ou insira uma quantia personalizada
Obrigado pela sua contribuição.
Faça uma doaçãoSabe-se que a taxa nominal de uma aplicação financeira é de 12% a.a., capitalizados mensalmente. Pede-se determinar:
a) quanto valerá uma aplicação de R$10.000,00 depois de 5 meses;
b) taxa efetiva anual da aplicação financeira;
c) taxa efetiva mensal da aplicação financeira.
Uma empresa contrata um empréstimo de R$48.700,00 e prazo de vencimento de 30 meses. Sendo a taxa de juro anual de 19,5% pede-se calcular o montante a pagar utilizando as convenções linear e exponencial.
Uma taxa efetiva de juros com capitalização quadrimestral é aplicada a um capital gerando um total de juros, ao final de 2 anos, igual a 270% do valor do capital aplicado. Determinar o valor desta taxa de juros.
Os rendimentasos de uma aplicação de R$12.800,00 somaram R$7.433,12 ao final de 36 meses. Determinar a taxa efetiva mensal de juros desta aplicação.
Uma loja está oferecendo uma mercadoria no valor de R$900,00 com desconto de 12% para pagamento a vista. Outra opção de compra é pagar os R$900,00 após 30 dias sem desconto. Calcular o custo efetivo mensal da venda a prazo.
Um banco publica em suas agências o seguinte anúncio: “aplique R$ 1.000,00 hoje e receba R$1.180,00 ao final de 6 mêses”. Determinar a efetiva taxa mensal, semestral e anual de juros oferecida por esta aplicação.
a) Um título está pagando uma taxa efetiva de 2,85% ao mês. Para um mês de 30 dias, transformar esta remuneração em taxa nominal (linear).
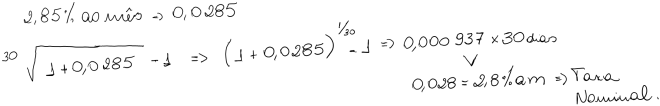
b) Para cada taxa nominal apresentada a seguir, pede-se calcular a taxa efetiva anual:
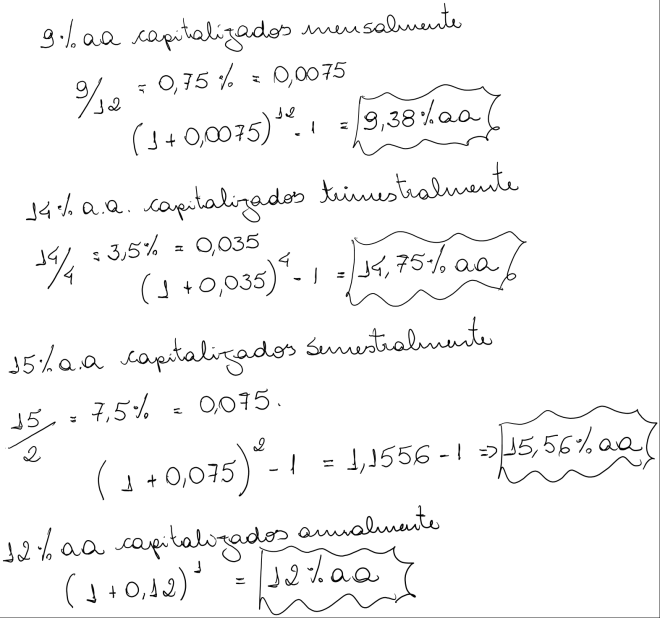
c) Calcular a taxa efetiva ao mês, dada a taxa nominal de 2% ao mês, capitalizada anualmente.
d) Calcule a taxa de juros efetiva semestral, equivalente à taxa de juros de 12% ao semestre, capitalizados trimestralmente.
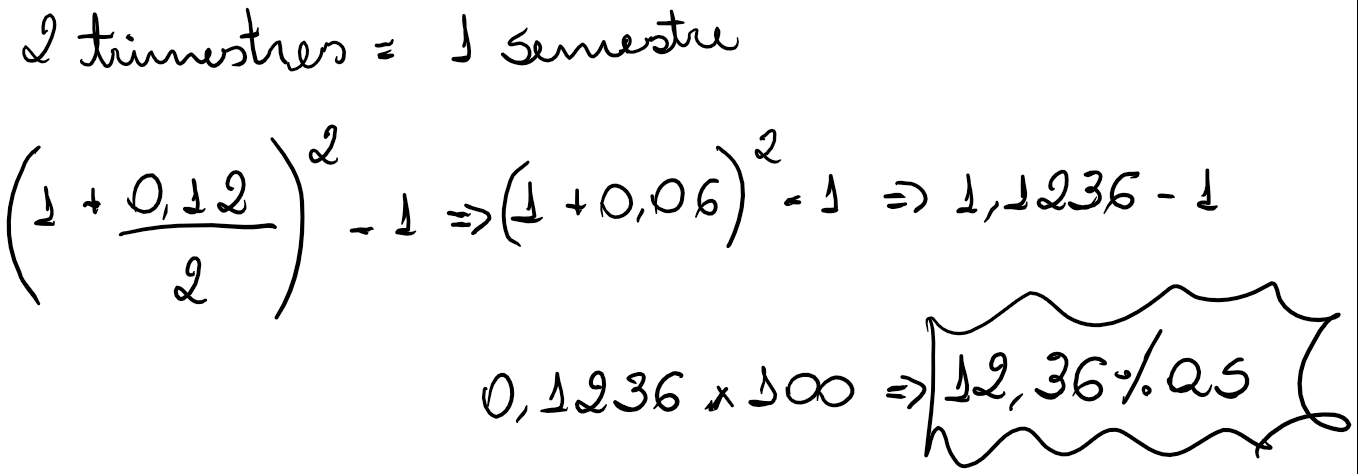
e) Transforme uma taxa efetiva de 12% semestral em mensal.
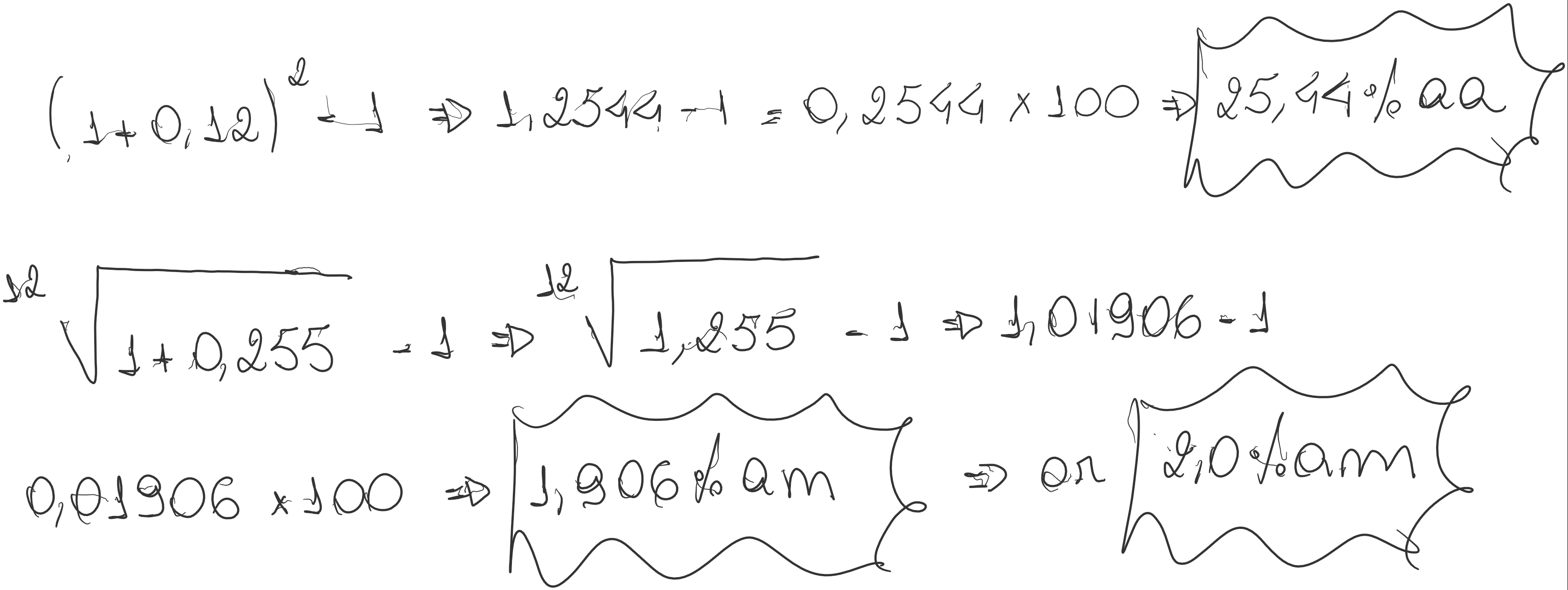
f) Para uma taxa nominal de 24% a a , calcule a taxa efetiva ao bimestre
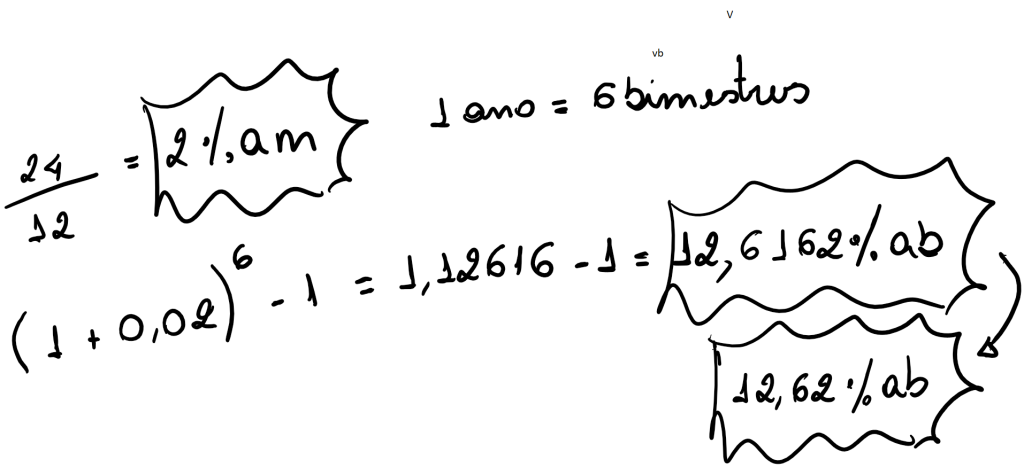
Um financiamento está sendo negociado a uma taxa nominal (linear) de 72% ao ano. Determinar o custo efetivo anual desta operação, admitindo-se que os juros sejam capitalizados:
a) mensalmente,
b) trimestralmente
c) semestralmente
Com relação a formação das taxas de juros, pede-se:
a) em 77 dias uma aplicação rendeu 8,3% de juros. Apurar as taxas mensal e anual equivalents.
b) um banco cobra anualmente 18,6% ao ano de juros. Para uma operação de 136 dias, determinar a taxa efetiva (equivalente) que será cobrada.
c) Uma empresa está cobrando juros de 3% para vendas a prazo de 28 dias corridos. Determinar a taxa efetiva mensal e anual da venda a prazo.
d) determinar a taxa equivalente para 44 dias de 109,3% ao ano.
Calcular a taxa equivalente mensal das seguintes taxas:
a) 2,9 % para 26 dias;
b) 3,55% para 34 dias.
Capitalizar as seguintes taxas:
a) 2,3% ao mês para um ano;
b) 0,14% ao dia para 23 dias;
c) 7,45% ao trimestre para um ano;
d) 6,75% ao semestre para um ano;
e) 1,87% equivalente a 20 dias para um ano
A taxa de juros de um financiamento está fixada em 3,3% a.m, em determinado momento. Qual o percentual desta taxa acumulada para um ano?
Quando se trata de taxa nominal é comum admitir-se que a capitalização ocorre por juros proporcionais simples. A taxa por período de capitalização de 36% ao ano é 3% ao mês. Aplica-se a taxa proporcional ou linear de juros simples (36% /12=3%).
Ao se capitalizar a taxa nominal de 36%aa, apura-se uma taxa efetiva de juros superior a 36% declarada na operação.
A formula para obter a Taxa Efetiva é :
Quando tratamos os juros de 36% ao ano , mas capitalizados mensalmente apura-se uma taxa efetiva de 42,6% ao ano.
Para que os 36% fosse considerada a taxa efetiva: A taxa mensal seria de 2,6% ao mês em vez de 3% ao mês. Para chegar neste valor teríamos que obter a taxa equivalente mensal de 36% ao ano.
Se multiplicarmos a taxa de 2,6%am por 12 meses = 31,2% ao ano.
31,2% é a taxa nominal, proporcional ou linear da operação.
Math Financeira 