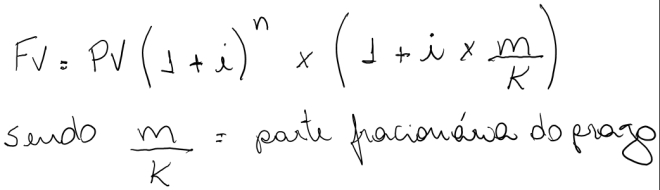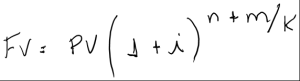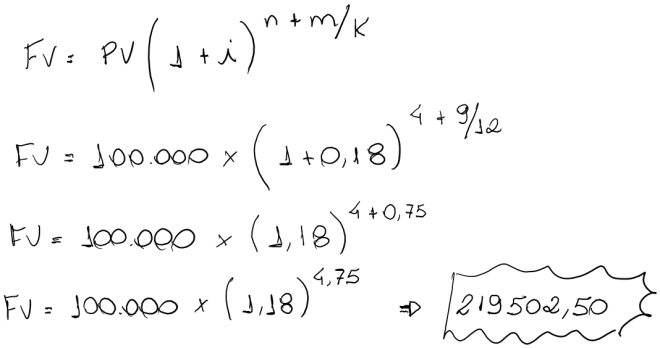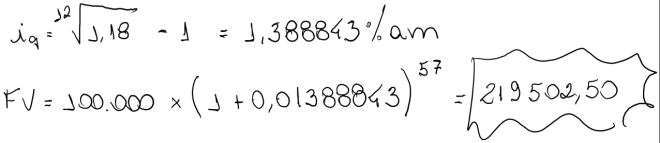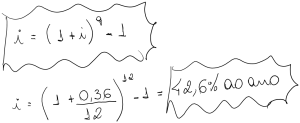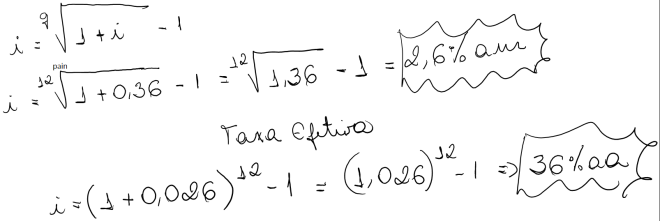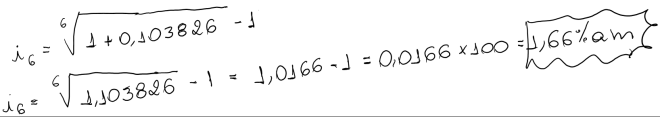Determinar as taxas mensal e anual equivalentes de juros de um capital de R$67.000,00 que produz um montante de R$171.929,17 ao final de 17 meses.
Categoria: Taxas Equivalentes – Juros Compostos
-

7) Juros Compostos – Taxa Efetiva e Taxa Equivalente- Exercício Proposto
Com relação a formação das taxas de juros, pede-se:
a) em 77 dias uma aplicação rendeu 8,3% de juros. Apurar as taxas mensal e anual equivalents.
b) um banco cobra anualmente 18,6% ao ano de juros. Para uma operação de 136 dias, determinar a taxa efetiva (equivalente) que será cobrada.
c) Uma empresa está cobrando juros de 3% para vendas a prazo de 28 dias corridos. Determinar a taxa efetiva mensal e anual da venda a prazo.
d) determinar a taxa equivalente para 44 dias de 109,3% ao ano.
-

5) Juros Compostos – Taxas Equivalentes – Exercício Proposto
Admita-se que um banco esteja pagando 16,5% ao ano de juros na colocação de um título de sua emissão. Apurar a taxa efetiva (equivalente) para os seguintes prazos.
a) 1 mês
b) 9 meses
c) 37 dias
d) 100 dias -

4) Juros Compostos – Taxas Equivalentes – Exercício Proposto
Se um investidor deseja ganhar 18% ao ano de taxa efetiva, pede-se calcular a taxa de juro que deverá exigir de uma aplicação se o prazo de capitalização for igual a :
a) 1 Mês;
b) 1 trimester;
c) 7 meses;
-

3) Juros Compostos – Taxas Equivalentes – Exercício Proposto
Calcular a taxa equivalente composta a 34% ao ano para os seguintes prazos:
a) 1 mês;
b) 1 quadrimestre
c) 1 semester
d) 5 meses
e) 10 meses
-

Convenção Linear e Convenção Exponencial Para Períodos Não Inteiros
Em algumas operações financeiras, o prazo não é um número inteiro em relação ao prazo definido para a taxa. Como na prática é muito raro a não-formação dos juros em intervalos de tempo inferiores a um período inteiro, passa-se adotar 2 convenções para solucionar estes casos: linear ou exponencial.
CONVENÇÃO LINEAR
Esta convenção é uma mistura do regime composto e linear, adotando formulas de juros compostos na parte inteira do período e uma formação de juros simples na parte fracionária.
Exemplo:
Seja o capital de R$100.000,00 emprestado à taxa de 18% ao ano pelo prazo de 4 anos e 9 meses. Calcular o montante deste empréstimo pela convenção linear.
Solução:
PV = 100.000,00
n (inteiro) = 4 anos
m/k (fracionário) = 9/12
I=18% ao ano
FV=?
Observação: O divisor da parte fracionária é 12 porque a parte inteira está sendo expressado anualmente (1 ano = 12 meses). A correspondência de 9 mêses em relação ao ano é 9/12=0,75 ano.
CONVENÇÃO EXPONENCIAL
Diferente da convenção linear, a convenção exponencial adota o regime de capitalização para todo o período. Esta convenção é mais usada porque emprega o juros compostos e taxas equivalentes para os períodos não inteiros. Tornando o valor mais próximo da realidade.
Utilizando- se os dados do exemplo anterior, calcula-se o montante:
O procedimento é o mesmo ao se determinar a taxa equivalente mensal de 18% ao ano e capitalizá-la para os 57 meses (4 anos e 9 meses)
n=4 anos e 9 meses = 57 meses
i=18% a.a.
CONCLUSÃO
Observa-se que existe uma diferença entre os montantes apurados:
FV (Conv. Linear) = 220.051,30
FV (Conv. Exponencial) = 219.502,50
220.051,30 – 219.502,50 = 548,80 (Diferença)
Eu te ajudei? Faça uma doação única para ajudar no meu trabalho.
Escolha um valor
R$5,00R$10,00R$15,00Ou insira uma quantia personalizada
R$
Obrigado pela sua contribuição.
Faça uma doação -

Taxa Nominal e Taxa Efetiva – Juros Compostos
Quando se trata de taxa nominal é comum admitir-se que a capitalização ocorre por juros proporcionais simples. A taxa por período de capitalização de 36% ao ano é 3% ao mês. Aplica-se a taxa proporcional ou linear de juros simples (36% /12=3%).
Ao se capitalizar a taxa nominal de 36%aa, apura-se uma taxa efetiva de juros superior a 36% declarada na operação.
A formula para obter a Taxa Efetiva é :
Quando tratamos os juros de 36% ao ano , mas capitalizados mensalmente apura-se uma taxa efetiva de 42,6% ao ano.
Para que os 36% fosse considerada a taxa efetiva: A taxa mensal seria de 2,6% ao mês em vez de 3% ao mês. Para chegar neste valor teríamos que obter a taxa equivalente mensal de 36% ao ano.
Se multiplicarmos a taxa de 2,6%am por 12 meses = 31,2% ao ano.
31,2% é a taxa nominal, proporcional ou linear da operação.
-

Taxas Equivalentes – Juros Compostos
O conceito enunciado de taxa equivalente permanence válido para o regime de juros compostos diferenciando-se dos juros simples na fómula de cálculo da taxa de juros. Por se tratar de capitalização exponencial, a expressão da taxa equivalente composta é a media geométrica da taxa de juros do período inteiro, isto é:
Por exemplo, a taxa equivalente composta mensal de 10,3826% ao semester é de 1,66% ao mês.
É equivalente para um mesmo capital e prazo de aplicação, o rendimento de 1,66% ao mês ou 10,3826% ao semestre
Para comprovar aplicaremos a formula de juros composto