Em algumas operações financeiras, o prazo não é um número inteiro em relação ao prazo definido para a taxa. Como na prática é muito raro a não-formação dos juros em intervalos de tempo inferiores a um período inteiro, passa-se adotar 2 convenções para solucionar estes casos: linear ou exponencial.
CONVENÇÃO LINEAR
Esta convenção é uma mistura do regime composto e linear, adotando formulas de juros compostos na parte inteira do período e uma formação de juros simples na parte fracionária.
Exemplo:
Seja o capital de R$100.000,00 emprestado à taxa de 18% ao ano pelo prazo de 4 anos e 9 meses. Calcular o montante deste empréstimo pela convenção linear.
Solução:
PV = 100.000,00
n (inteiro) = 4 anos
m/k (fracionário) = 9/12
I=18% ao ano
FV=?
Observação: O divisor da parte fracionária é 12 porque a parte inteira está sendo expressado anualmente (1 ano = 12 meses). A correspondência de 9 mêses em relação ao ano é 9/12=0,75 ano.
CONVENÇÃO EXPONENCIAL
Diferente da convenção linear, a convenção exponencial adota o regime de capitalização para todo o período. Esta convenção é mais usada porque emprega o juros compostos e taxas equivalentes para os períodos não inteiros. Tornando o valor mais próximo da realidade.
Utilizando- se os dados do exemplo anterior, calcula-se o montante:
O procedimento é o mesmo ao se determinar a taxa equivalente mensal de 18% ao ano e capitalizá-la para os 57 meses (4 anos e 9 meses)
n=4 anos e 9 meses = 57 meses
i=18% a.a.
CONCLUSÃO
Observa-se que existe uma diferença entre os montantes apurados:
FV (Conv. Linear) = 220.051,30
FV (Conv. Exponencial) = 219.502,50
220.051,30 – 219.502,50 = 548,80 (Diferença)
Eu te ajudei? Faça uma doação única para ajudar no meu trabalho.
Escolha um valor
Ou insira uma quantia personalizada
Obrigado pela sua contribuição.
Faça uma doação
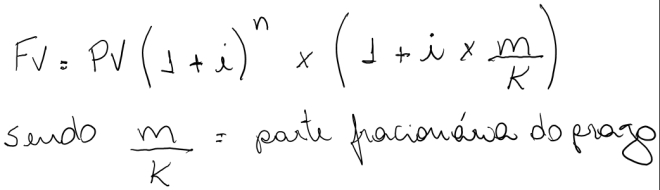

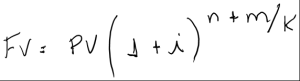
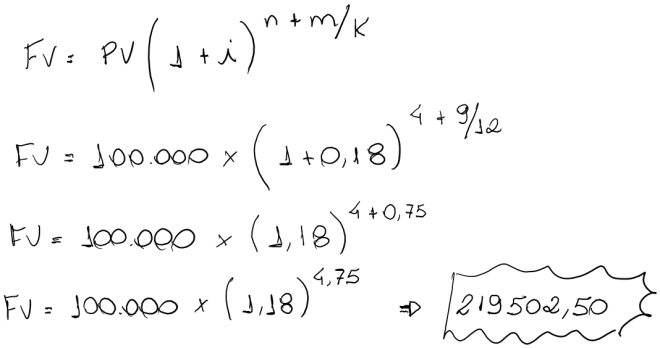
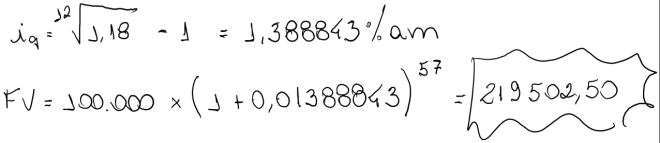
Deixar mensagem para Prof. Flávio Moita Cancelar resposta