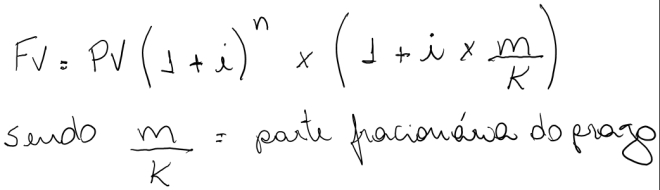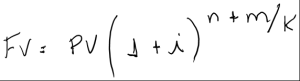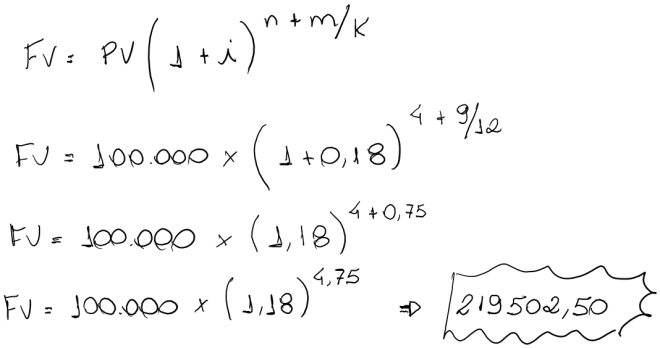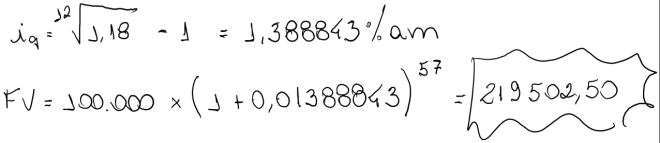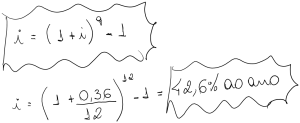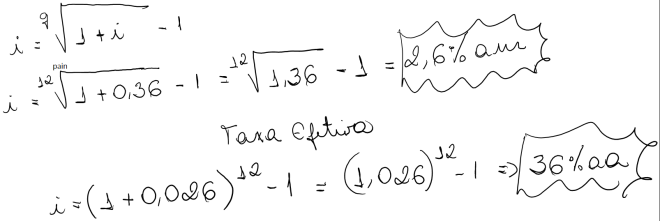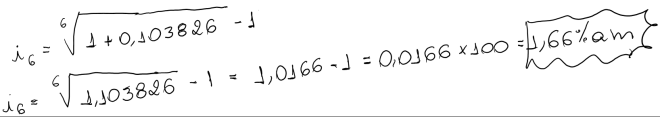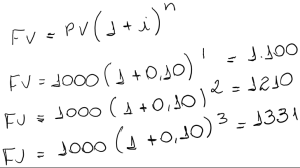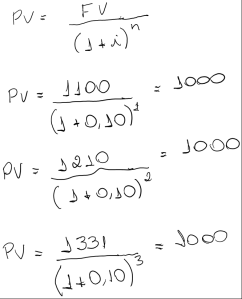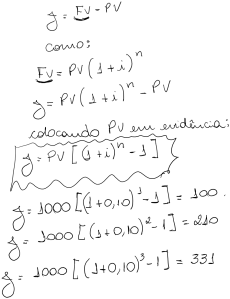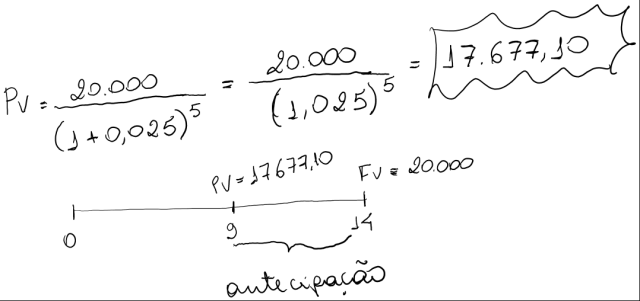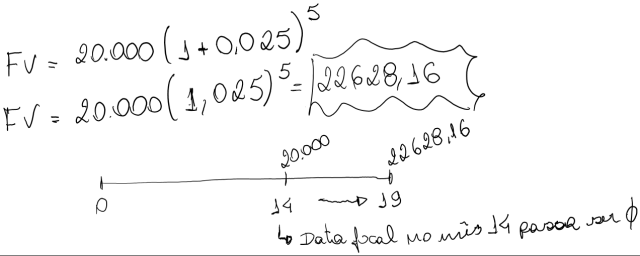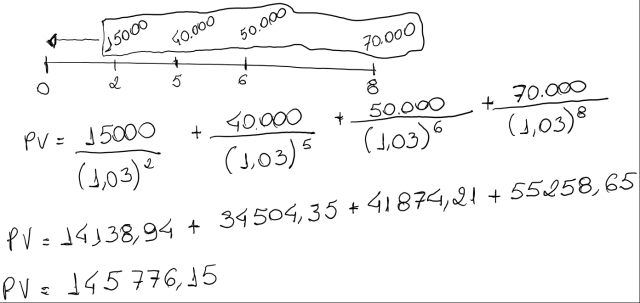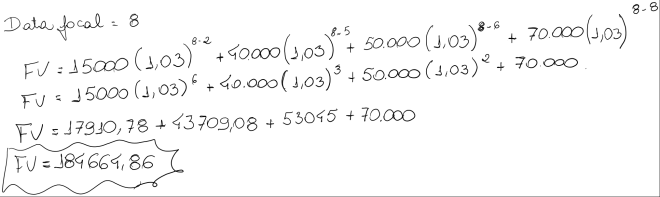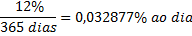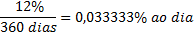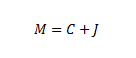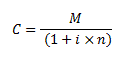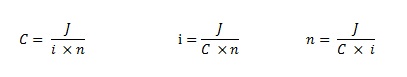Math Financeira

Categoria: Assuntos

Conceitos e explicações dos tópicos da matemática financeira abordados nos exercícios deste site.

  • Aplicando Juros Simples na prática

    Aplicando Juros Simples na prática

    Os valores de juros e multa adotados, na maioria dos casos, por magistrados e Advogados no Brasil são baseados nos Juros Simples com percentual de 1% ao mês.

    Na prática irei demonstrar através de exemplos, a forma para calcular o saldo devedor aplicando a fómula do Juros Simples.

    Considere a relação abaixo que demonstra os vencimentos de cada boleto e seus respectivos pagamentos:

    Boleto Nome do Pagador Vencimento Pagamento Valor do Boleto Dias de Atraso Valor de Juros
    34191.75074 96625.012529 50451.630003 3 00000000000001 Ricardo Lacerda 05/01/2011 22/01/2015 R$         765,00 1478 R$   1.141,89
    34191.75074 96625.012529 50451.630003 3 00000000000002 Ricardo Lacerda 05/02/2010 05/03/2015 R$         765,00 1854 R$   1.237,77
    34191.75074 96625.012529 50451.630003 3 00000000000003 Ricardo Lacerda 05/03/2009 07/04/2015 R$         765,00 2224 R$   1.332,12
    34191.75074 96625.012529 50451.630003 3 00000000000004 Ricardo Lacerda 06/04/2015 16/05/2015 R$         765,00 40 R$       775,20
    Taxa de Juros ao dia 0,000333333 Total a Pagar: R$   4.486,98

    Considerando Juros de 1% ao mês é necessário modificar a periodicidade dos pagamentos para o fator Dia. Assim transformando 1% ao mês para dia e considerando que o mês tem 30 dias temos:

    TAXA=1/100=0,01

    TAXA=0,01/30 dias=0,000333333

    Utilizando  a  formula de juros simples: M =Cx(1+ i x n)

    M=VALOR DO BOLETO x(1+TAXA x NUMERO DE DIAS DE ATRASO)

    Onde :

    N= Número de dias de atraso | i=Taxa | C= Capital que deveria ser pago

    Valor do Boleto Dias de Atraso Valor de Juros Fórmula Cálculo
    R$           765,00 1478 R$   1.141,89 Cx(1+ixn) 765x(1+0,000333333×1478)
    R$           765,00 1854 R$   1.237,77 Cx(1+ixn) 765x(1+0,000333333×1854)
    R$           765,00 2224 R$   1.332,12 Cx(1+ixn) 765x(1+0,000333333×2224)
    R$           765,00 40 R$       775,20 Cx(1+ixn) 765x(1+0,000333333×40)
    Total a Pagar: R$   4.486,98
  • Convenção Linear e Convenção Exponencial Para Períodos Não Inteiros

    Convenção Linear e Convenção Exponencial Para Períodos Não Inteiros

    Em algumas operações financeiras, o prazo não é um número inteiro em relação ao prazo definido para a taxa. Como na prática é muito raro a não-formação dos juros em intervalos de tempo inferiores a um período inteiro, passa-se adotar 2 convenções para solucionar estes casos: linear ou exponencial.

    CONVENÇÃO LINEAR

    Esta convenção é uma mistura do regime composto e linear, adotando formulas de juros compostos na parte inteira do período e uma formação de juros simples na parte fracionária.

    composto18

    Exemplo:

    Seja o capital de R$100.000,00 emprestado à taxa de 18% ao ano pelo prazo de 4 anos e 9 meses. Calcular o montante deste empréstimo pela convenção linear.

    Solução:

    PV = 100.000,00

    n (inteiro) = 4 anos

    m/k (fracionário) = 9/12

    I=18% ao ano

    FV=?

    Observação: O divisor da parte fracionária é 12 porque a parte inteira está sendo expressado anualmente (1 ano = 12 meses). A correspondência de 9 mêses em relação ao ano é 9/12=0,75 ano.

    composto19

    CONVENÇÃO EXPONENCIAL

    Diferente da convenção linear, a convenção exponencial adota o regime de capitalização para todo o período. Esta convenção é mais usada porque emprega o juros compostos e taxas equivalentes para os períodos não inteiros. Tornando o valor mais próximo da realidade.

    composto20

    Utilizando- se os dados do exemplo anterior, calcula-se o montante:

    composto21

    O procedimento é o mesmo ao se determinar a taxa equivalente mensal de 18% ao ano e capitalizá-la para os 57 meses (4 anos e 9 meses)

    n=4 anos e 9 meses = 57 meses

    i=18% a.a.

    composto22

    CONCLUSÃO

    Observa-se que existe uma diferença entre os montantes apurados:

    FV (Conv. Linear) = 220.051,30

    FV (Conv. Exponencial) = 219.502,50

    220.051,30 – 219.502,50 = 548,80 (Diferença)

    Eu te ajudei? Faça uma doação única para ajudar no meu trabalho.

    Escolha um valor

    R$5,00
    R$10,00
    R$15,00

    Ou insira uma quantia personalizada

    R$

    Obrigado pela sua contribuição.

    Faça uma doação
  • Taxa Nominal e Taxa Efetiva – Juros Compostos

    Taxa Nominal e Taxa Efetiva – Juros Compostos

    Quando se trata de taxa nominal é comum admitir-se que a capitalização ocorre por juros proporcionais simples. A taxa por período de capitalização de 36% ao ano é 3% ao mês. Aplica-se a taxa proporcional ou linear de juros simples (36% /12=3%).

    Ao se capitalizar a taxa nominal de 36%aa, apura-se uma taxa efetiva de juros superior a 36% declarada na operação.

    A formula para obter a Taxa Efetiva é :

    composto13

    Quando tratamos os juros de 36% ao ano , mas capitalizados mensalmente apura-se uma taxa efetiva de 42,6% ao ano.

    Para que os 36% fosse considerada a taxa efetiva: A taxa mensal seria de 2,6% ao mês em vez de 3% ao mês. Para chegar neste valor teríamos que obter a taxa equivalente mensal de 36% ao ano.

    composto15

    Se multiplicarmos a taxa de 2,6%am por 12 meses = 31,2% ao ano.

    31,2% é a taxa nominal, proporcional ou linear da operação.

  • Taxas Equivalentes – Juros Compostos

    Taxas Equivalentes – Juros Compostos

    O conceito enunciado de taxa equivalente permanence válido para o regime de juros compostos diferenciando-se dos juros simples na fómula de cálculo da taxa de juros. Por se tratar de capitalização exponencial, a expressão da taxa equivalente composta é a media geométrica da taxa de juros do período inteiro, isto é:

    composto9

    Por exemplo, a taxa equivalente composta mensal de 10,3826% ao semester é de 1,66% ao mês.

    composto10

    É equivalente para um mesmo capital e prazo de aplicação, o rendimento de 1,66% ao mês ou 10,3826% ao semestre

    Para comprovar aplicaremos a formula de juros composto

    composto11

  • Juros Compostos

    Juros Compostos

    O regime de juros compostos considera que os juros formados em cada período são acrescidos ao capital formando o montante (capital + juros) do período, ou seja, o montante passará a render juros no período seguinte formando um novo montante (constituído do capital inicial, dos juros acumulados e dos juros sobre os juros formados em períodos anteriores), e assim por diante.

    Mês Capital + Juros (PV) Taxa Montante (FV)
    0 1000 10% 1100
    1 1100 10% 1210
    2 1210 10% 1331
    3 1331 10% 1464,1

    grafico

    Antes de definir a formula do cálculo do juros composto é bom entender a seguinte prática:

    1a Condição) Quando queremos acrescentar 10% do valor de 1000 então: 1000 x (1+ 0,10)= 1100

    2a Condição) Quando queremos diminuir 10% do valor de 1000 entã0: 1000 x (100%-10%) = 1000 x 0,9 = 900

    3a Condição) Quando queremos 10% do valor de 1000 então temos 1000 x 0,10 = 100

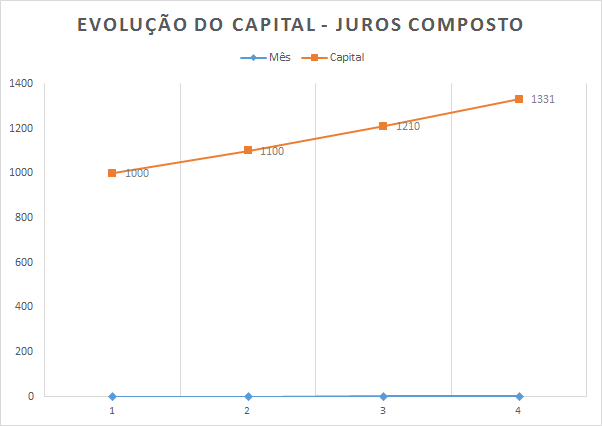
    O juros compostos basea-se na primeira condição acima e concluindo este raciocínio, temos a tabela acima modificada da seguinte forma:

    Mês Taxa Cálculo Montante
    1 10% FV= 1000 x (1+0,10) 1100
    2 10% FV= 1000 x (1+0,10) x(1+0,10) 1210
    3 10% FV= 1000 x (1+0,10) x(1+0,10) x (1+0,10) 1331
    4 10% FV= 1000 x (1+0,10) x(1+0,10) x (1+0,10) x … 1464,1

    Percebe-se que o que repete no cálculo é a expressão (1+0,10) proporcional ao mês? No mês 1 repete 1 vez, no mês dois repete 2 vezes e assim por diante?

    Então concluímos e generalizamos que a formula para calcular o juros composto é:

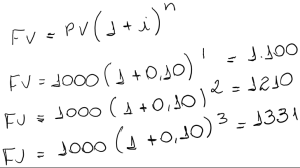
    composto

    Concluímos que aplicando o capital de R$1000,00 à uma taxa mensal de 10% ao mês durante 3 mêses o montante seria de R$1331,00 gerando para o investidor um rendimento de R$331,00 de juros. Os juros então é o valor monetário (R$331,00) que é apurado pela diferença entre o montante FV (R$1331,00) e o capital PV (R$1000,00).

    A formula acima é utilizada quando queremos saber o valor futuro, ou seja, qual o montante que terei se caso investir um valor ou adquirir uma dívida a um prazo e taxa definida.

    Quando queremos saber o valor no presente do montante no futuro temos a seguinte variação da formula acima:

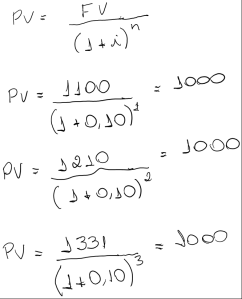
    composto2

    Concluímos que para conseguir chegar à R$1331,00 em 3 mêses à uma taxa de 10% ao mês teremos que desembolsar R$1000,00 no tempo presente.

    Voltando aos juros adquiridos pelo investidor de R$331,00 citado acima, podemos obter o resultado também pela seguinte expressão:

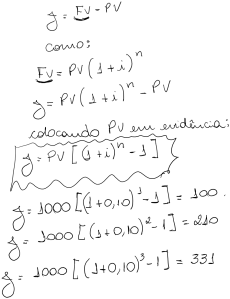
    composto3

    Nem sempre o valor presente é expressado no momento zero, ele pode ser apurado em qualquer data focal anterior à do valor futuro (montante). É muito comum em casos de antecipar a dívida.

    Por exemplo: deseja-se calcular quanto será pago por um empréstimo de R$20.000,00 vencíveis de hoje a 14 mêses ao se antecipar por 5 mêses a data do seu pagamento. Sabe-se que o credor está disposto a atualizar a dívida à taxa composta de 2,5% ao mês.

    Neste exemplo é preciso ficar atento que no momento presente a pessoa gostaria de saber para quanto cairia sua dívida se ela antecipasse. Como regra vamos adotar a formula do valor presente sempre quando tiver um valor atualizado a uma data anterior à do montante (mês 9). Logo:

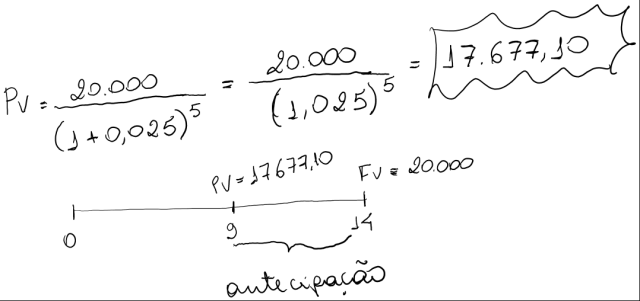
    composto4

    No exemplo acima se a pessoa quizesse prolongar a sua dívida para 19 mêses a formula mudaria para:

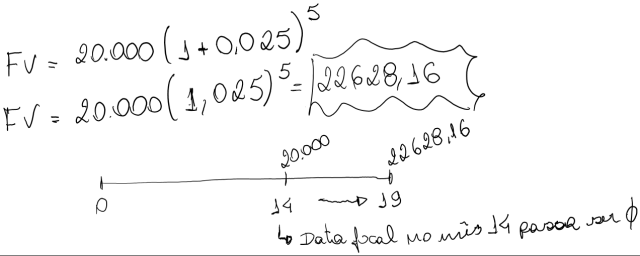
    composto7

    É importante saber que as expressões de cálculos de PV e FV permitem capitalizações e atualizações envolvendo diversos valores e não somente um único capital ou montante.

    Considere um empréstimo que envolve os seguintes pagamentos: R$15.000,00 de hoje a 2 meses; R$40.000,00 de hoje a 5 meses; R$50.000,00 de hoje a 6 meses e R$70.000,00 de hoje a 8 meses. O devedor deseja pagar e liquidar as dívidas, no presente (na data zero). A taxa de juros considerada nesta antecipação é de 3% ao mês. Temos com Data Focal = 0

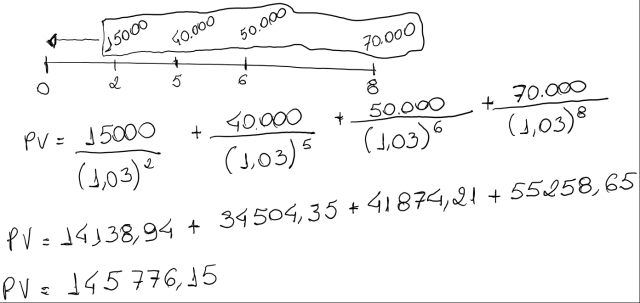
    composto8

    Consideramos este mesmo exemplo definindo o mês 8 como data focal:

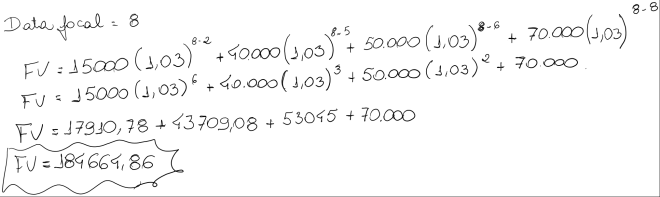
    composto16

    EQUIVALÊNCIA FINANCEIRA – JUROS COMPOSTOS

    Temos um conjunto de compromissos financeiros e gostaríamos de trocar por outro equivalente. Temos dois empréstimos e por dificuldades financeiras queremos substituir estas dívidas por outra devendo-se determinar o valor de pagamento no mês 12 a uma taxa de juros de 2% ao mês..

    Pagamento original: 50.000,00 (no quarto mês) e 80.000,00 (no oitavo mês)

    Proposta de pagamento: 10.000,00 de entrada, 30.000,00 (no sexto mês) e o restante no ultimo mês.

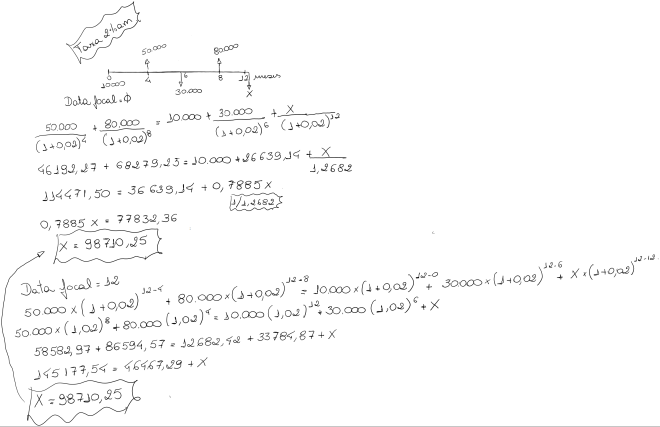
    composto17

    Repare que o saldo a pagar não se altera com a data focal. Em juros compostos a equivalência financeira independe do momento tomado como comparação.

  • Juro Exato e Juro Comercial – Juros Simples versus Juros Compostos

    Juro Exato e Juro Comercial – Juros Simples versus Juros Compostos

    É comum nas operações de curto prazo, onde predominam as aplicações com taxas referenciais em juros simples e compostos, ter-se o prazo definido em número dias. Nestes casos, o número de dias pode ser calculado de duas maneiras:

    a) Pelo tempo exato, utilizando -se efetivamente o calendário do ano civil (365 dias). O Juro apurado desta maneira denomina-se juro exato.

    b) pelo ano comercial, o qual admite o mês com 30 dias e o ano com 360 dias. Tem-se, por este critério, a apuração do denominado juro comercial ou ordinário.

    Por exempo, 12% ao ano equivale no regime de juros simples a taxa diária seria de :

    a) Juro Exato:

    b) Juro Comercial:

    Por exempo, 12% ao ano equivale no regime de juros compostos a taxa diária seria de :

    a) Juro Exato:

    b) Juro Comercial:

    Eu te ajudei? Faça uma doação única para ajudar no meu trabalho.

    Escolha um valor

    R$5,00
    R$10,00
    R$15,00

    Ou insira uma quantia personalizada

    R$

    Obrigado pela sua contribuição.

    Faça uma doação
  • Taxa Proporcional e Taxa Equivalente – Juros Simples

    Taxa Proporcional e Taxa Equivalente – Juros Simples

    No regime de juros simples, diante de sua própria natureza linear, esta transformação é processada pela denominada taxa proporcional de juros também denominada de taxa linear ou nominal.  Esta taxa proporcional é obtida da divisão entre a taxa de juros considerada na operação e o número de vezes em que ocorrerão os juros (quantidade de períodos de capitalização).

    Por exemplo: Para taxa de juros de 19% ao ano , se a capitalização for definida mensalmente (ocorrerão 12 vezes juros no período de um ano), o percentual de juros que incidirá sobre o capital a cada mês será:

    As taxas de juros simples se dizem equivalente  quando, aplicadas a um mesmo capital e pelo mesmo intervalo de tempo, produzem o mesmo volume linear de juros.

    Por exemplo, em juros simples, um capital de R$500.000,00, se aplicado a 2,5% ao mês ou 15% ao semestre pelo prazo de um ano, produz o mesmo montante linear de juros. Isto é:

  • Montante e Capital – Juros Simples

    Montante e Capital – Juros Simples

    Um determinado capital, quando aplicado a uma taxa periódica de juro por determinado tempo, produz um valor acumulado denominado de montante, e identificado em juros simples por M. Em outras palavras, o montante é constituído do capital mais o valor acumulado dos juros, isto é:


    No entanto, sabe-se que:


     Substituindo esta expressão básica na fórmula do montante supra, e colocando-se C em evidência:

    Evidentemente, o valor de C desta fórmula pode ser obtido através de simples transformação algébrica:

    A expressão (1 + i  x  n)  é definida como fator de capitalização (ou de valor futuro – FCS) dos juros simples. Ao multiplicar um capital por este valor, corrige-se o seu valor para uma data futura, determinando o montante. O Inverso, ou seja, 1/(1 + i x n) é denominado de fator de atualização (ou de valor presente – FAS). Ao se aplicar o fator sobre um valor expresso em uma data futura, apura-se o seu equivalente numa data atual.

  • Fórmulas de Juros Simples

    Fórmulas de Juros Simples

     

    O valor dos Juros é calculado a partir da seguinte expressão:

    onde:

    j =valor dos juros expresso em unidades monetárias;

    C =capital. É o valor (em $) representativo de determinado momento;

    i =taxa de juros, expressa em sua forma unitária;

    n=prazo.

    Esta fórmula é básica tanto para o cálculo dos juros como dos outros valores financeiros mediante simples dedução algébrica.