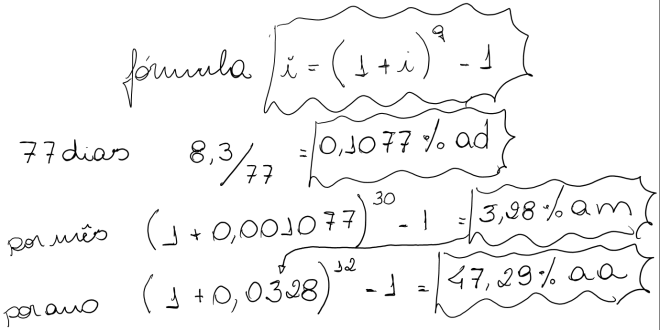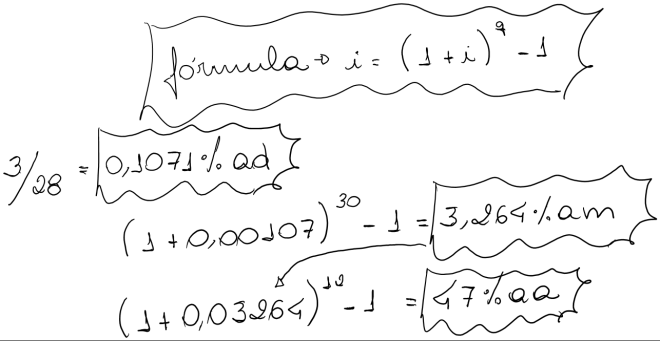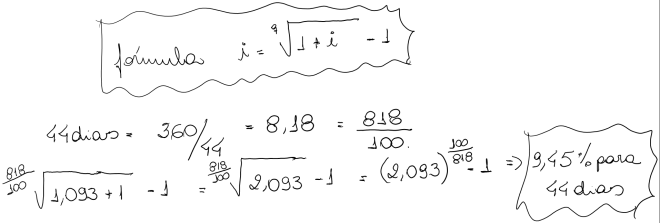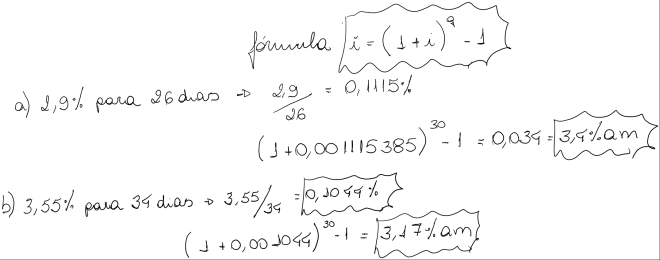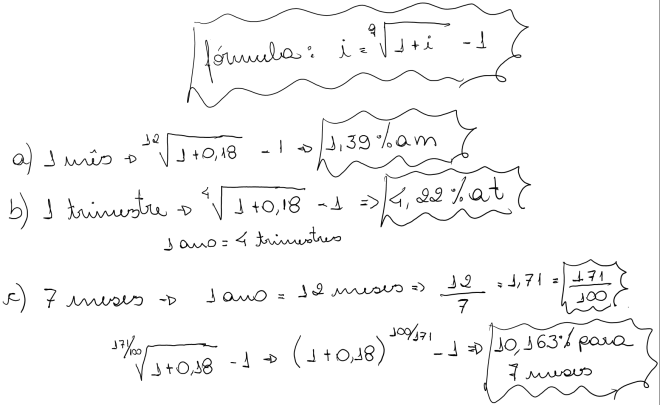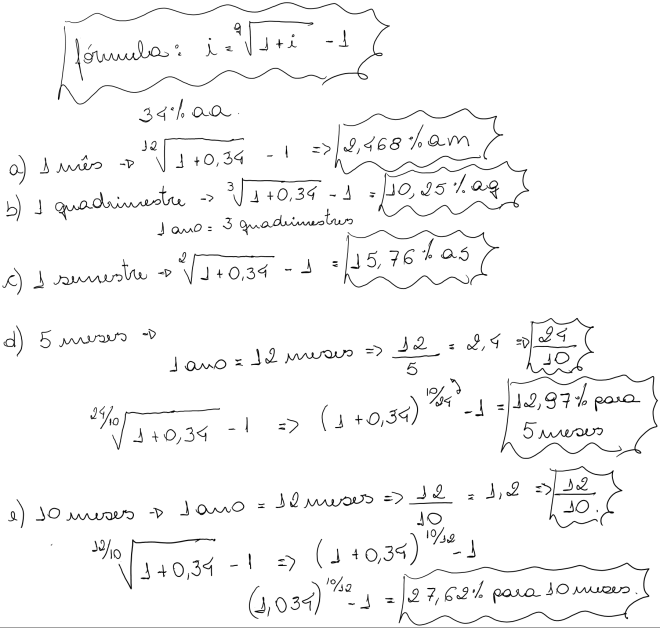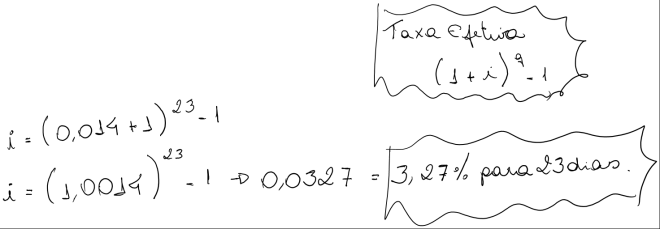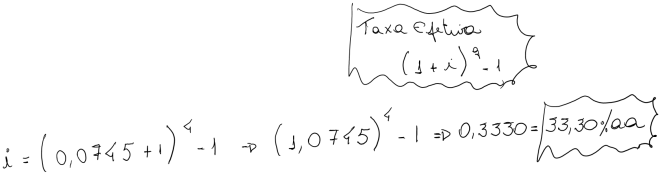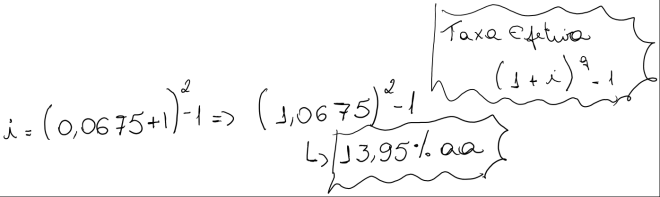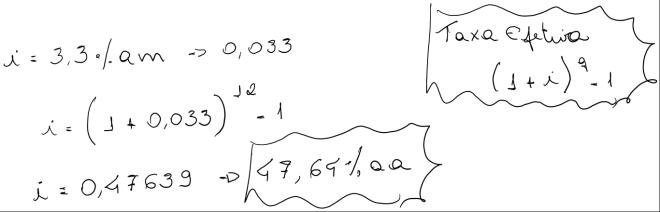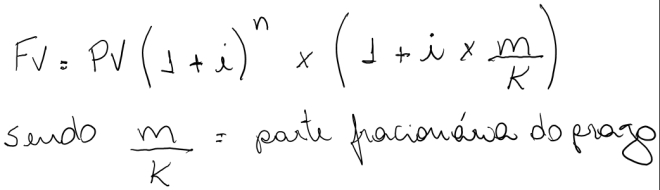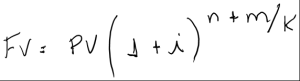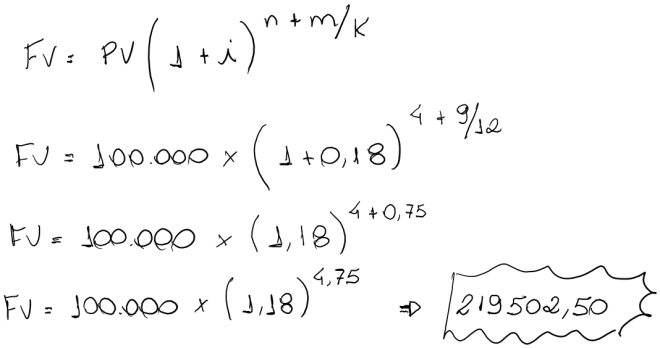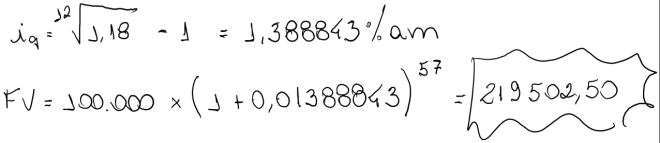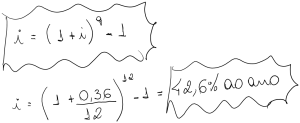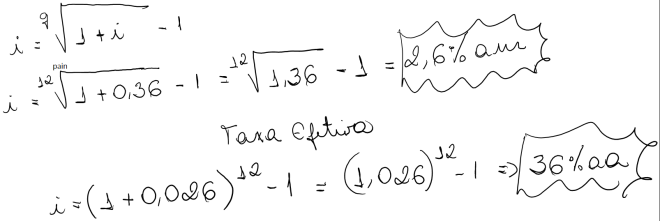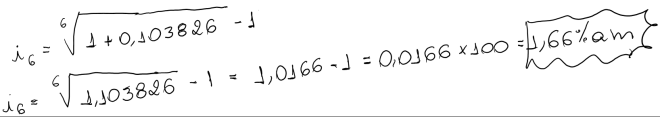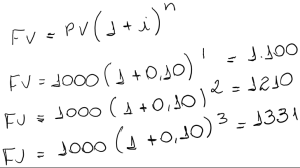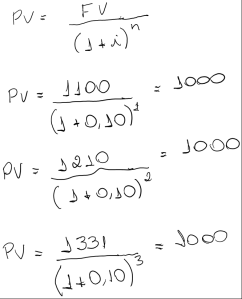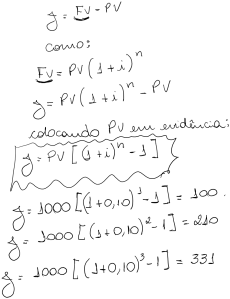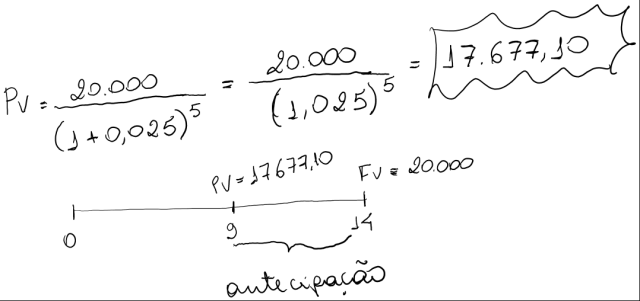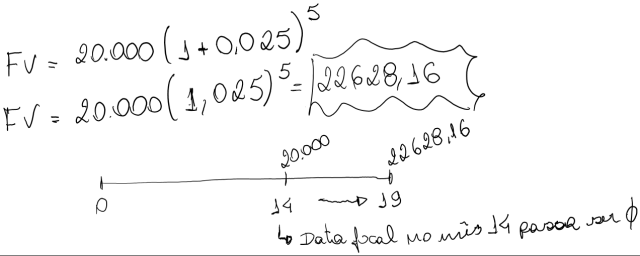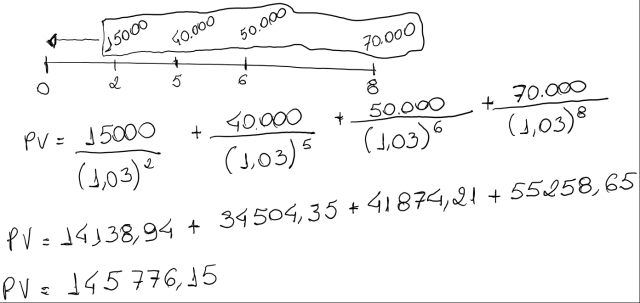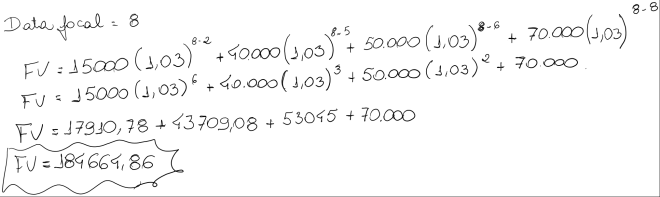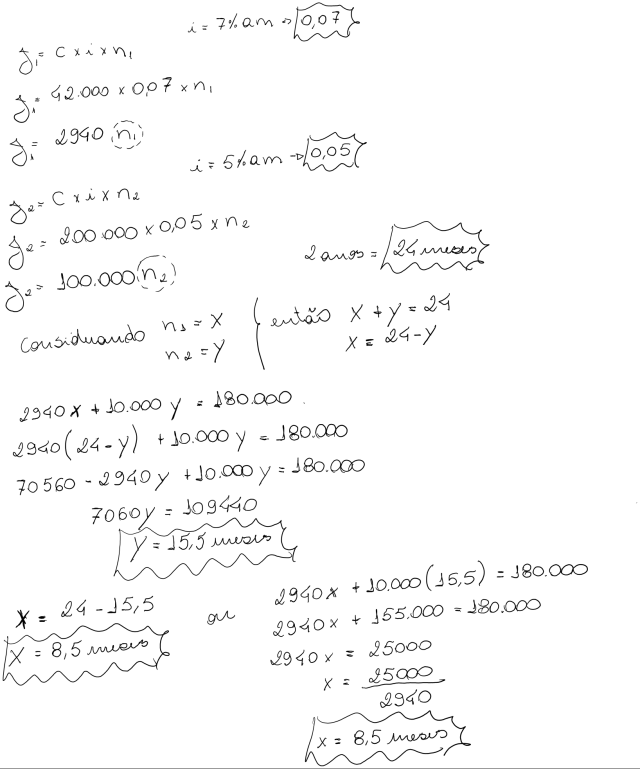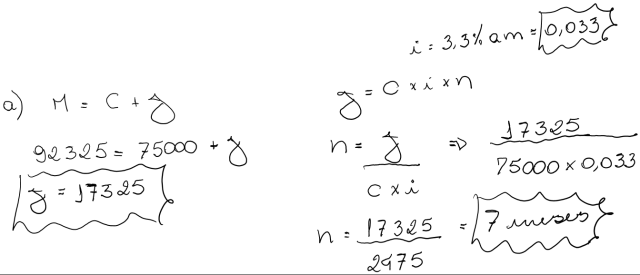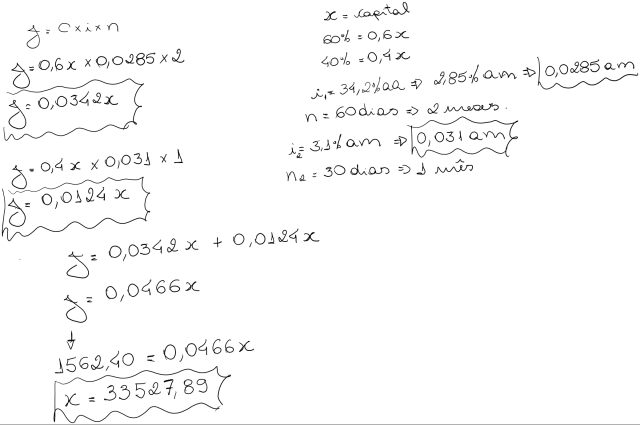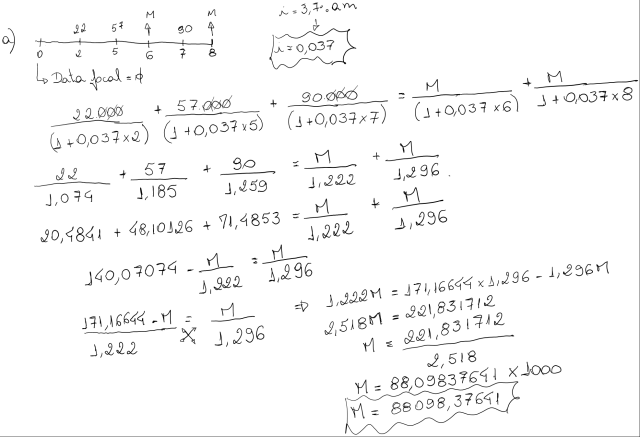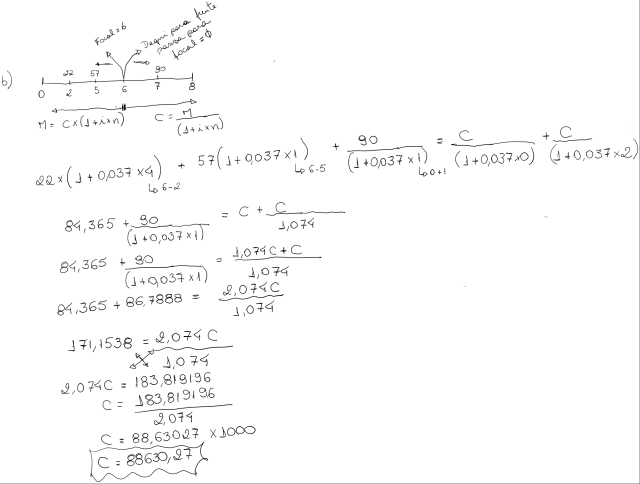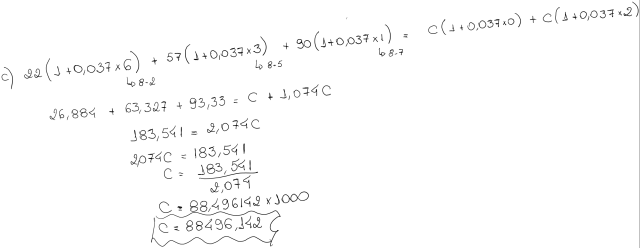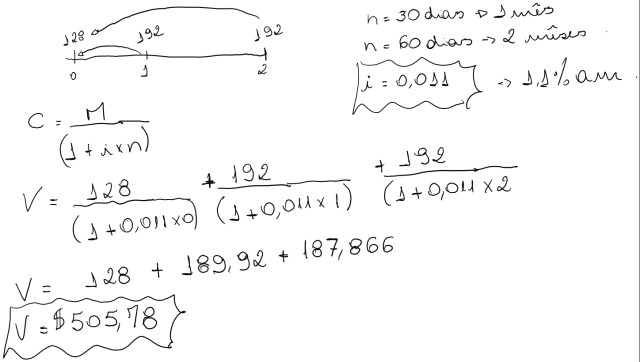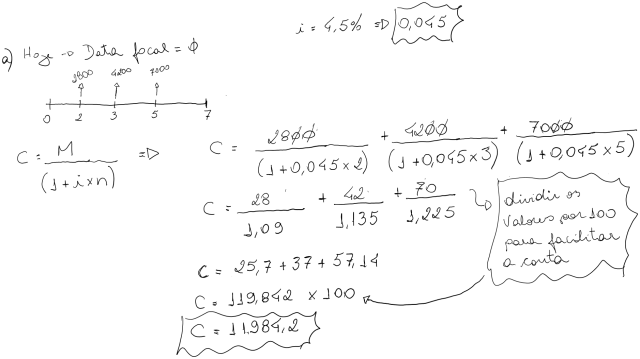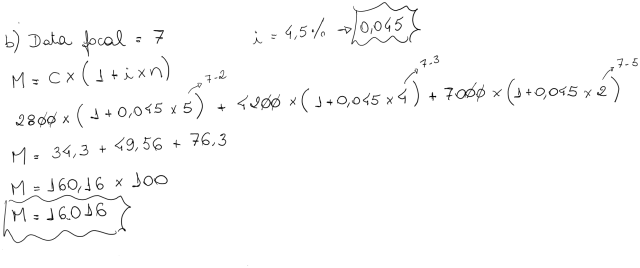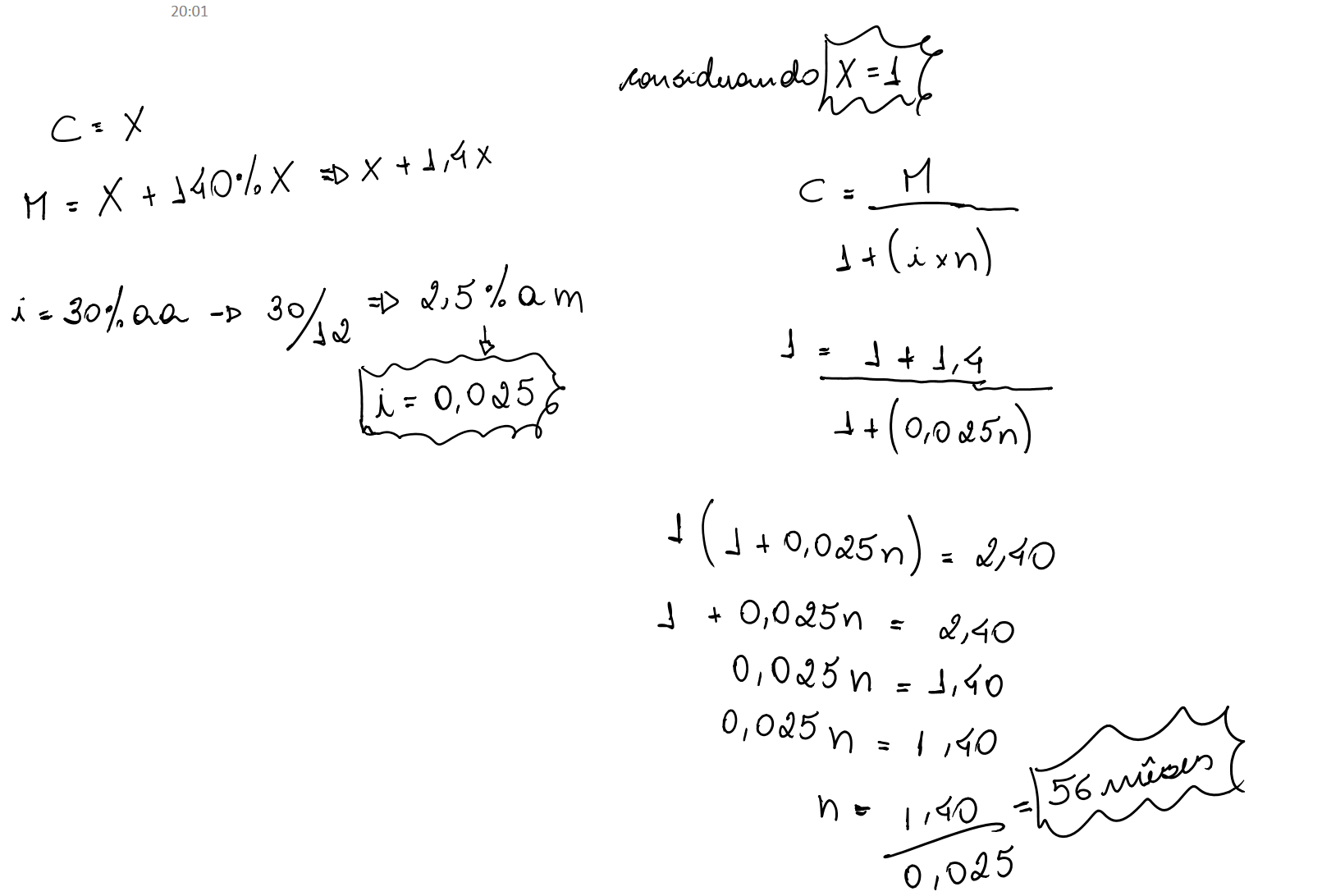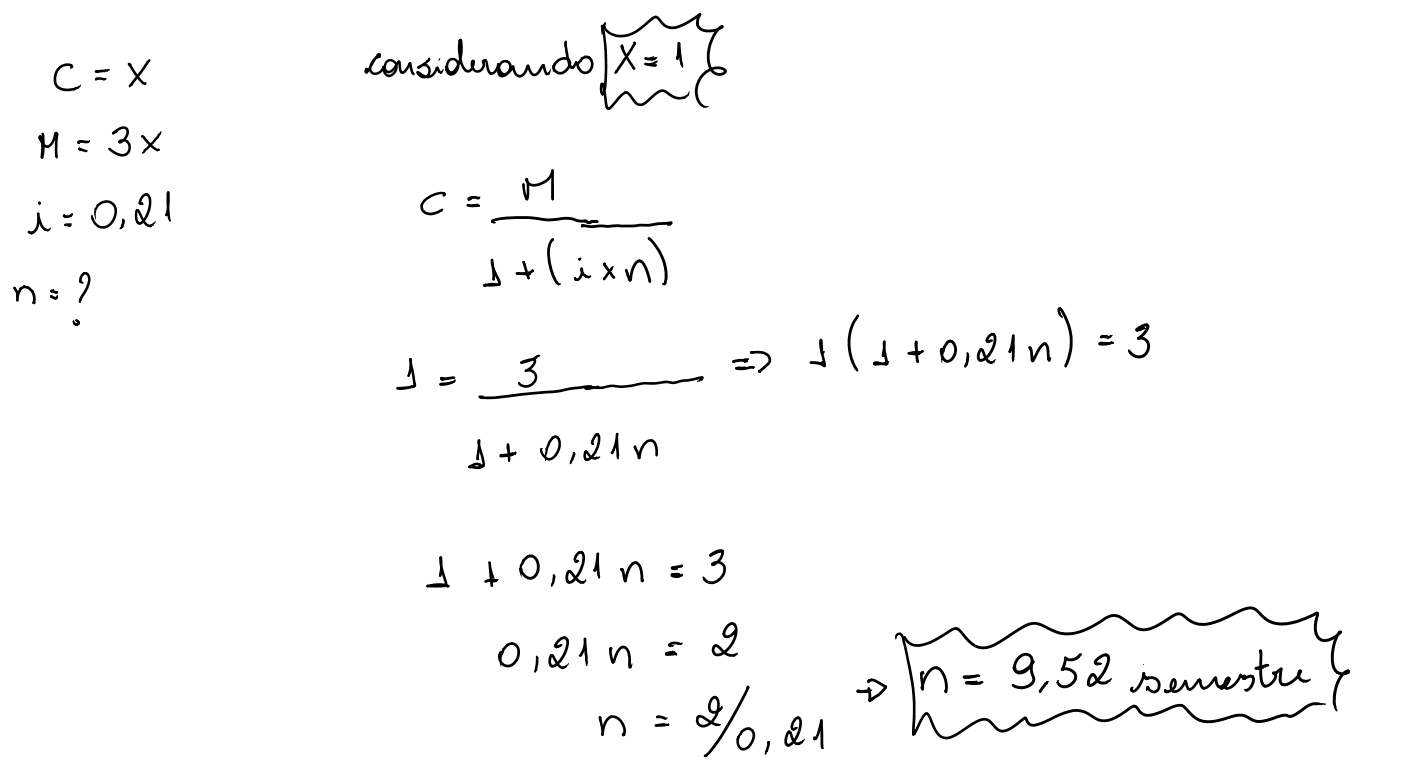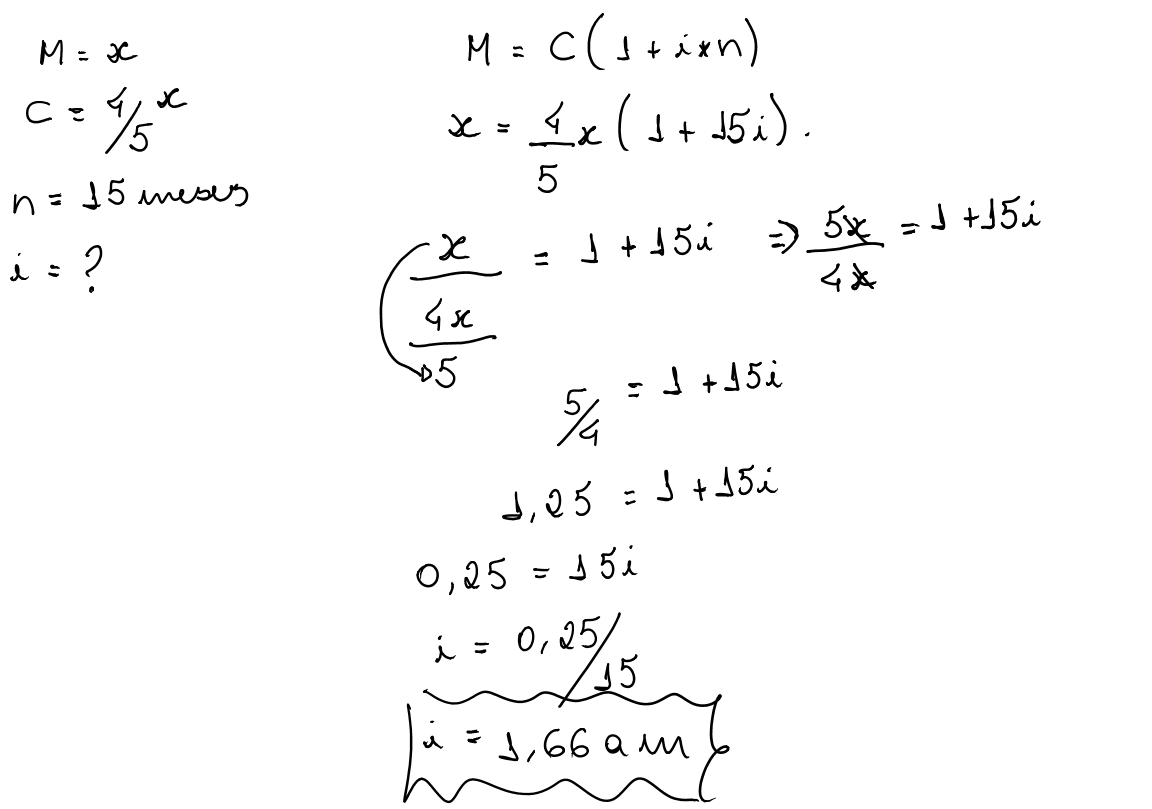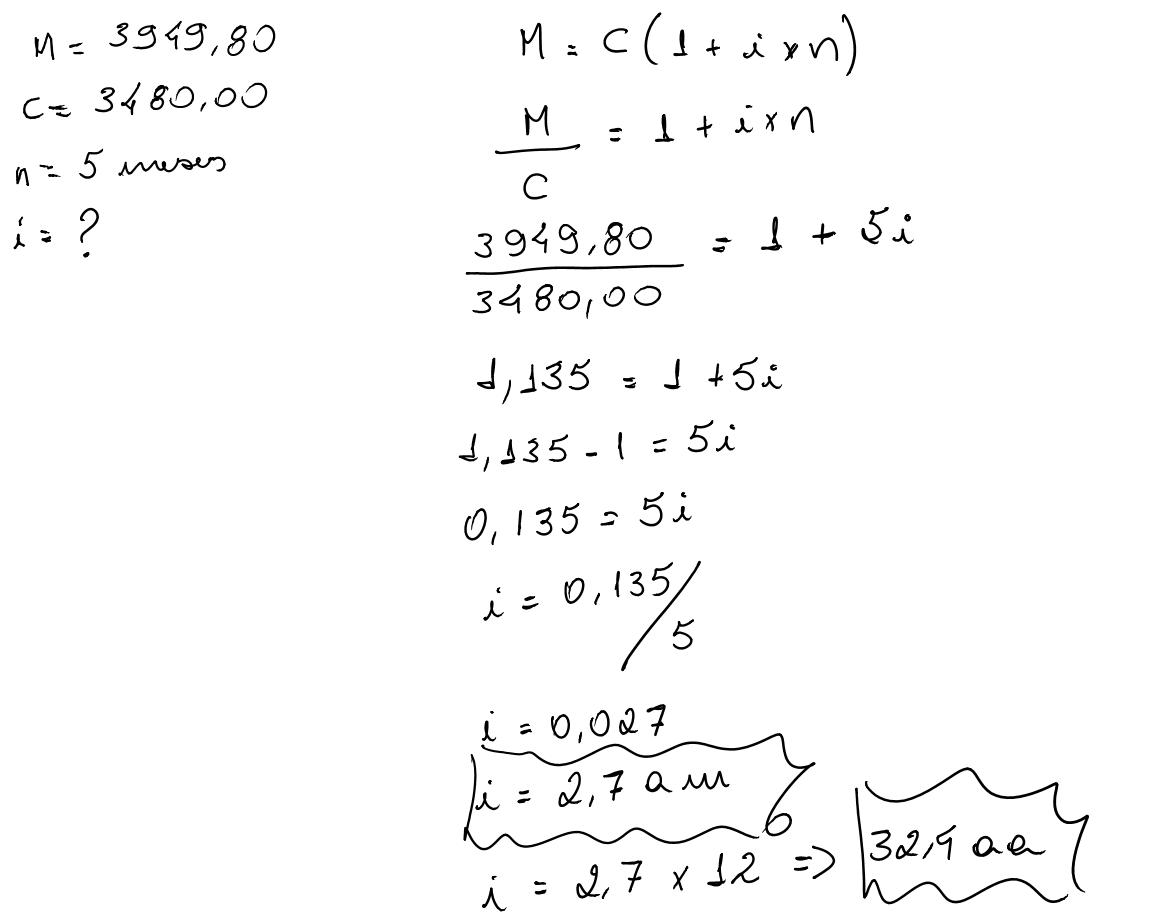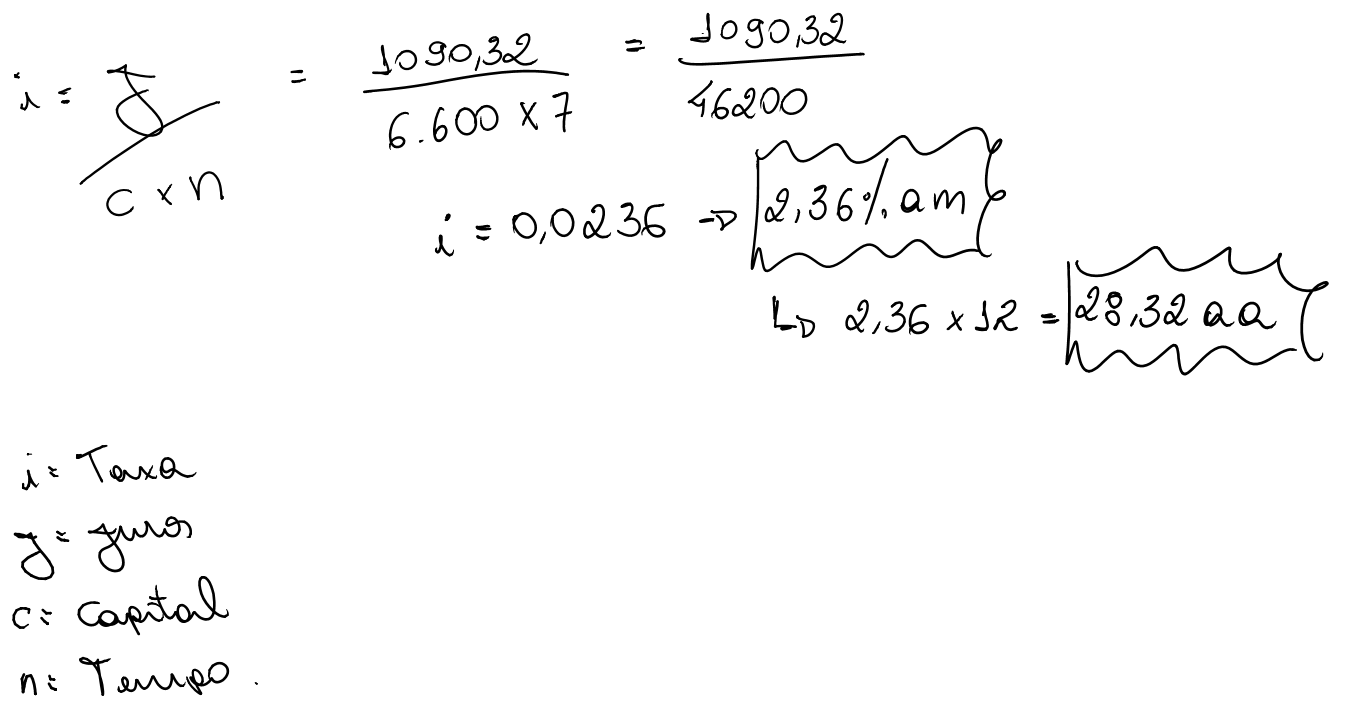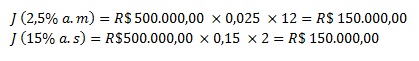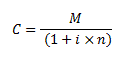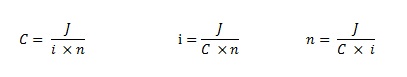Calcular a taxa mensal de juros de uma aplicação de R$68.700,00 que produz um montante de R$82.084,90 ao final de 8 meses.
Blog
-
13) Juros Compostos – Exercício Proposto
Sendo a taxa corrente de juros de 10% ao a.q. (ao quadrimestre), quando deve ser aplicado hoje para se resgatar R$38.500,00 daqui a 28 meses?
n= 28 meses/4 quadrimestres = 7 quadrimestres
-
12) Juros Compostos – Exercício Proposto
Um banco lança um título pagando 6% ao trimestre. Se uma pessoa necessitar de R$58.000,00 daqui a 3 anos, quanto deverá aplicar neste título?
-
11) Juros Compostos – Exercício Proposto
Calcular o juro de uma aplicação de R$300.000,00 nas seguintes condições de prazo e taxa:
- I=2,5% a.m.
- n=1 semestre
- I=3,3% a.m
- n= 1 ano e 3 meses
- i = 6% a.s.
- n= 72 meses
- I= 10% a.a
- n= 120 meses
- I=2,5% a.q
- n= 4 anos
-
10) Juros Compostos – Exercício Proposto
Determinar o montante de uma aplicação de R$22.000,00 admitindo os seguintes prazos e taxas:
- i= 2,2% a.m
- n= 7 meses
- i= 5% a.m.
- n= 2 anos
- i= 2,2% a.t.
- n= 1 ano e meio
- i= 20% a.s.
- n= 4 anos
- i=0,15% ao dia.
- n=47 dias
- i=9% a.a.
- n=216 meses
-
9) Juros Compostos – Converter Taxa Efetiva e Taxa Nominal – Exercício Proposto
a) Um título está pagando uma taxa efetiva de 2,85% ao mês. Para um mês de 30 dias, transformar esta remuneração em taxa nominal (linear).
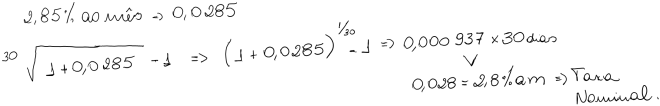
b) Para cada taxa nominal apresentada a seguir, pede-se calcular a taxa efetiva anual:
- 9% a.a. capitalizados mensalmente
- 14% a.a. capitalizados trimestralmente
- 15% a.a. capitalizados semestralmente.
- 12% a.a. capitalizados anualmente.
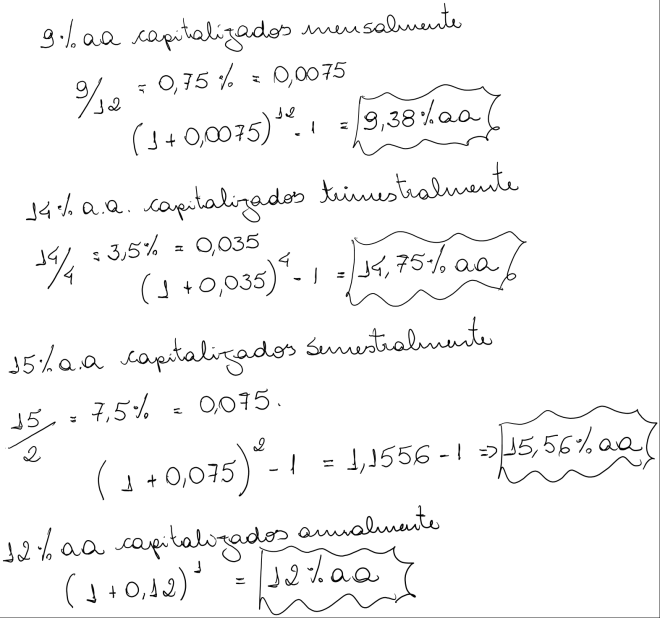
c) Calcular a taxa efetiva ao mês, dada a taxa nominal de 2% ao mês, capitalizada anualmente.
d) Calcule a taxa de juros efetiva semestral, equivalente à taxa de juros de 12% ao semestre, capitalizados trimestralmente.
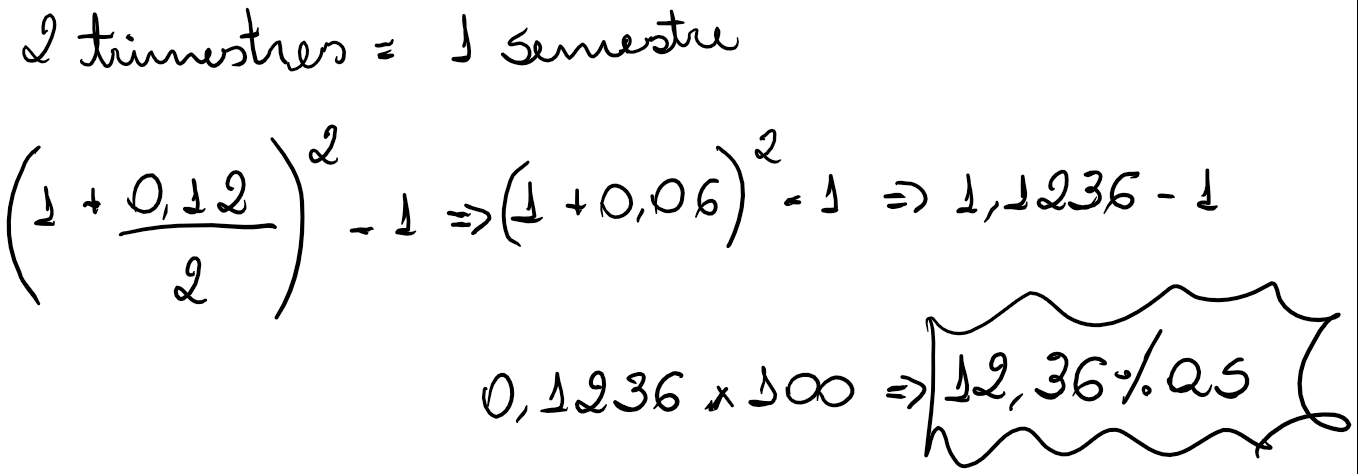
e) Transforme uma taxa efetiva de 12% semestral em mensal.
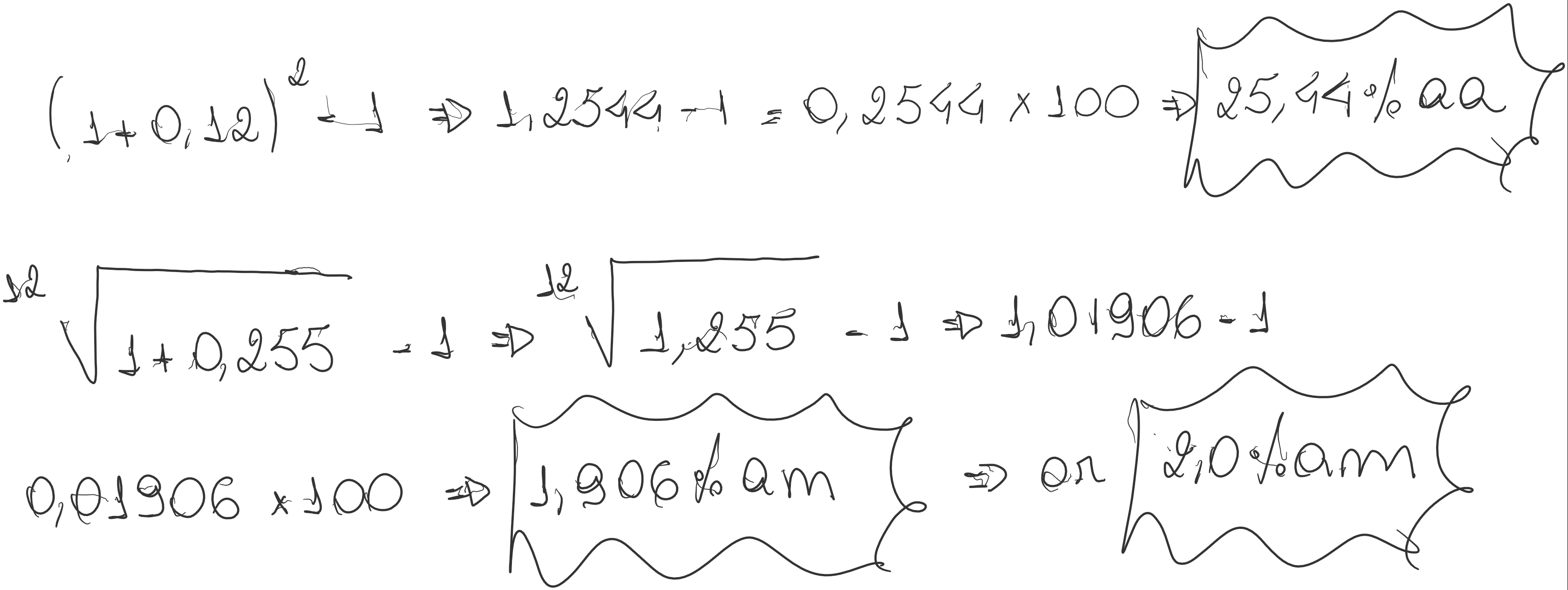
f) Para uma taxa nominal de 24% a a , calcule a taxa efetiva ao bimestre
-
8) Juros Compostos – Taxa Nominal (Linear) – Exercício Proposto
Um financiamento está sendo negociado a uma taxa nominal (linear) de 72% ao ano. Determinar o custo efetivo anual desta operação, admitindo-se que os juros sejam capitalizados:
a) mensalmente,
b) trimestralmente
c) semestralmente
-
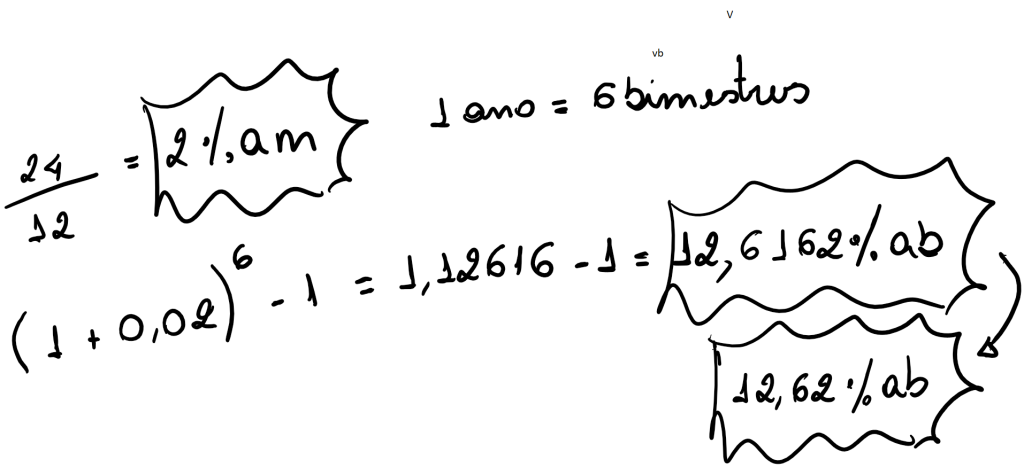
7) Juros Compostos – Taxa Efetiva e Taxa Equivalente- Exercício Proposto
Com relação a formação das taxas de juros, pede-se:
a) em 77 dias uma aplicação rendeu 8,3% de juros. Apurar as taxas mensal e anual equivalents.
b) um banco cobra anualmente 18,6% ao ano de juros. Para uma operação de 136 dias, determinar a taxa efetiva (equivalente) que será cobrada.
c) Uma empresa está cobrando juros de 3% para vendas a prazo de 28 dias corridos. Determinar a taxa efetiva mensal e anual da venda a prazo.
d) determinar a taxa equivalente para 44 dias de 109,3% ao ano.
-
6) Juros Compostos – Taxa Efetiva – Exercício Proposto
Calcular a taxa equivalente mensal das seguintes taxas:
a) 2,9 % para 26 dias;
b) 3,55% para 34 dias.
-
5) Juros Compostos – Taxas Equivalentes – Exercício Proposto
Admita-se que um banco esteja pagando 16,5% ao ano de juros na colocação de um título de sua emissão. Apurar a taxa efetiva (equivalente) para os seguintes prazos.
a) 1 mês
b) 9 meses
c) 37 dias
d) 100 dias
-
4) Juros Compostos – Taxas Equivalentes – Exercício Proposto
Se um investidor deseja ganhar 18% ao ano de taxa efetiva, pede-se calcular a taxa de juro que deverá exigir de uma aplicação se o prazo de capitalização for igual a :
a) 1 Mês;
b) 1 trimester;
c) 7 meses;
-
3) Juros Compostos – Taxas Equivalentes – Exercício Proposto
Calcular a taxa equivalente composta a 34% ao ano para os seguintes prazos:
a) 1 mês;
b) 1 quadrimestre
c) 1 semester
d) 5 meses
e) 10 meses
-
2) Juros Compostos – Taxa Efetiva – Exercício Proposto
Capitalizar as seguintes taxas:
a) 2,3% ao mês para um ano;
b) 0,14% ao dia para 23 dias;
c) 7,45% ao trimestre para um ano;
d) 6,75% ao semestre para um ano;
e) 1,87% equivalente a 20 dias para um ano
-
1) Juros Compostos – Taxa Efetiva – Exercício Proposto
A taxa de juros de um financiamento está fixada em 3,3% a.m, em determinado momento. Qual o percentual desta taxa acumulada para um ano?
-
Convenção Linear e Convenção Exponencial Para Períodos Não Inteiros
Em algumas operações financeiras, o prazo não é um número inteiro em relação ao prazo definido para a taxa. Como na prática é muito raro a não-formação dos juros em intervalos de tempo inferiores a um período inteiro, passa-se adotar 2 convenções para solucionar estes casos: linear ou exponencial.
CONVENÇÃO LINEAR
Esta convenção é uma mistura do regime composto e linear, adotando formulas de juros compostos na parte inteira do período e uma formação de juros simples na parte fracionária.
Exemplo:
Seja o capital de R$100.000,00 emprestado à taxa de 18% ao ano pelo prazo de 4 anos e 9 meses. Calcular o montante deste empréstimo pela convenção linear.
Solução:
PV = 100.000,00
n (inteiro) = 4 anos
m/k (fracionário) = 9/12
I=18% ao ano
FV=?
Observação: O divisor da parte fracionária é 12 porque a parte inteira está sendo expressado anualmente (1 ano = 12 meses). A correspondência de 9 mêses em relação ao ano é 9/12=0,75 ano.
CONVENÇÃO EXPONENCIAL
Diferente da convenção linear, a convenção exponencial adota o regime de capitalização para todo o período. Esta convenção é mais usada porque emprega o juros compostos e taxas equivalentes para os períodos não inteiros. Tornando o valor mais próximo da realidade.
Utilizando- se os dados do exemplo anterior, calcula-se o montante:
O procedimento é o mesmo ao se determinar a taxa equivalente mensal de 18% ao ano e capitalizá-la para os 57 meses (4 anos e 9 meses)
n=4 anos e 9 meses = 57 meses
i=18% a.a.
CONCLUSÃO
Observa-se que existe uma diferença entre os montantes apurados:
FV (Conv. Linear) = 220.051,30
FV (Conv. Exponencial) = 219.502,50
220.051,30 – 219.502,50 = 548,80 (Diferença)
Eu te ajudei? Faça uma doação única para ajudar no meu trabalho.
Escolha um valor
R$5,00R$10,00R$15,00Ou insira uma quantia personalizada
R$
Obrigado pela sua contribuição.
Faça uma doação -
Taxa Nominal e Taxa Efetiva – Juros Compostos
Quando se trata de taxa nominal é comum admitir-se que a capitalização ocorre por juros proporcionais simples. A taxa por período de capitalização de 36% ao ano é 3% ao mês. Aplica-se a taxa proporcional ou linear de juros simples (36% /12=3%).
Ao se capitalizar a taxa nominal de 36%aa, apura-se uma taxa efetiva de juros superior a 36% declarada na operação.
A formula para obter a Taxa Efetiva é :
Quando tratamos os juros de 36% ao ano , mas capitalizados mensalmente apura-se uma taxa efetiva de 42,6% ao ano.
Para que os 36% fosse considerada a taxa efetiva: A taxa mensal seria de 2,6% ao mês em vez de 3% ao mês. Para chegar neste valor teríamos que obter a taxa equivalente mensal de 36% ao ano.
Se multiplicarmos a taxa de 2,6%am por 12 meses = 31,2% ao ano.
31,2% é a taxa nominal, proporcional ou linear da operação.
-
Taxas Equivalentes – Juros Compostos
O conceito enunciado de taxa equivalente permanence válido para o regime de juros compostos diferenciando-se dos juros simples na fómula de cálculo da taxa de juros. Por se tratar de capitalização exponencial, a expressão da taxa equivalente composta é a media geométrica da taxa de juros do período inteiro, isto é:
Por exemplo, a taxa equivalente composta mensal de 10,3826% ao semester é de 1,66% ao mês.
É equivalente para um mesmo capital e prazo de aplicação, o rendimento de 1,66% ao mês ou 10,3826% ao semestre
Para comprovar aplicaremos a formula de juros composto
-
Juros Compostos
O regime de juros compostos considera que os juros formados em cada período são acrescidos ao capital formando o montante (capital + juros) do período, ou seja, o montante passará a render juros no período seguinte formando um novo montante (constituído do capital inicial, dos juros acumulados e dos juros sobre os juros formados em períodos anteriores), e assim por diante.
Mês Capital + Juros (PV) Taxa Montante (FV) 0 1000 10% 1100 1 1100 10% 1210 2 1210 10% 1331 3 1331 10% 1464,1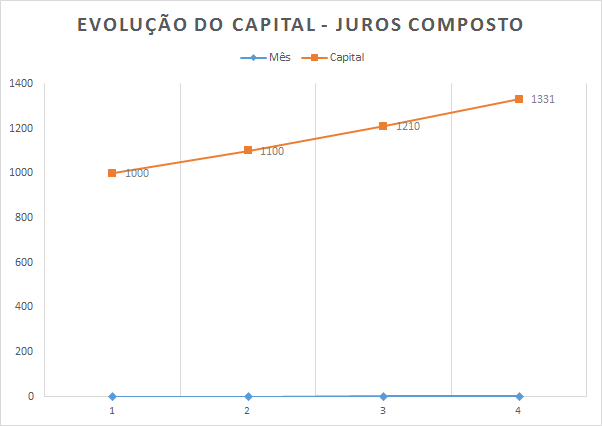 
Antes de definir a formula do cálculo do juros composto é bom entender a seguinte prática:
1a Condição) Quando queremos acrescentar 10% do valor de 1000 então: 1000 x (1+ 0,10)= 1100
2a Condição) Quando queremos diminuir 10% do valor de 1000 entã0: 1000 x (100%-10%) = 1000 x 0,9 = 900
3a Condição) Quando queremos 10% do valor de 1000 então temos 1000 x 0,10 = 100
O juros compostos basea-se na primeira condição acima e concluindo este raciocínio, temos a tabela acima modificada da seguinte forma:
Mês Taxa Cálculo Montante 1 10% FV= 1000 x (1+0,10) 1100 2 10% FV= 1000 x (1+0,10) x(1+0,10) 1210 3 10% FV= 1000 x (1+0,10) x(1+0,10) x (1+0,10) 1331 4 10% FV= 1000 x (1+0,10) x(1+0,10) x (1+0,10) x … 1464,1 Percebe-se que o que repete no cálculo é a expressão (1+0,10) proporcional ao mês? No mês 1 repete 1 vez, no mês dois repete 2 vezes e assim por diante?
Então concluímos e generalizamos que a formula para calcular o juros composto é:
Concluímos que aplicando o capital de R$1000,00 à uma taxa mensal de 10% ao mês durante 3 mêses o montante seria de R$1331,00 gerando para o investidor um rendimento de R$331,00 de juros. Os juros então é o valor monetário (R$331,00) que é apurado pela diferença entre o montante FV (R$1331,00) e o capital PV (R$1000,00).
A formula acima é utilizada quando queremos saber o valor futuro, ou seja, qual o montante que terei se caso investir um valor ou adquirir uma dívida a um prazo e taxa definida.
Quando queremos saber o valor no presente do montante no futuro temos a seguinte variação da formula acima:
Concluímos que para conseguir chegar à R$1331,00 em 3 mêses à uma taxa de 10% ao mês teremos que desembolsar R$1000,00 no tempo presente.
Voltando aos juros adquiridos pelo investidor de R$331,00 citado acima, podemos obter o resultado também pela seguinte expressão:
Nem sempre o valor presente é expressado no momento zero, ele pode ser apurado em qualquer data focal anterior à do valor futuro (montante). É muito comum em casos de antecipar a dívida.
Por exemplo: deseja-se calcular quanto será pago por um empréstimo de R$20.000,00 vencíveis de hoje a 14 mêses ao se antecipar por 5 mêses a data do seu pagamento. Sabe-se que o credor está disposto a atualizar a dívida à taxa composta de 2,5% ao mês.
Neste exemplo é preciso ficar atento que no momento presente a pessoa gostaria de saber para quanto cairia sua dívida se ela antecipasse. Como regra vamos adotar a formula do valor presente sempre quando tiver um valor atualizado a uma data anterior à do montante (mês 9). Logo:
No exemplo acima se a pessoa quizesse prolongar a sua dívida para 19 mêses a formula mudaria para:
É importante saber que as expressões de cálculos de PV e FV permitem capitalizações e atualizações envolvendo diversos valores e não somente um único capital ou montante.
Considere um empréstimo que envolve os seguintes pagamentos: R$15.000,00 de hoje a 2 meses; R$40.000,00 de hoje a 5 meses; R$50.000,00 de hoje a 6 meses e R$70.000,00 de hoje a 8 meses. O devedor deseja pagar e liquidar as dívidas, no presente (na data zero). A taxa de juros considerada nesta antecipação é de 3% ao mês. Temos com Data Focal = 0
Consideramos este mesmo exemplo definindo o mês 8 como data focal:
EQUIVALÊNCIA FINANCEIRA – JUROS COMPOSTOS
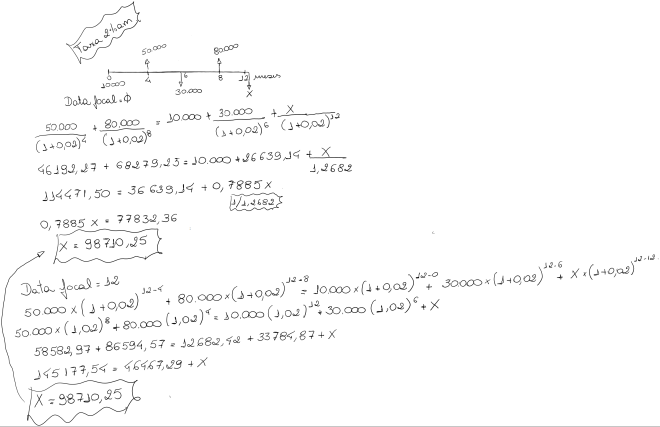
Temos um conjunto de compromissos financeiros e gostaríamos de trocar por outro equivalente. Temos dois empréstimos e por dificuldades financeiras queremos substituir estas dívidas por outra devendo-se determinar o valor de pagamento no mês 12 a uma taxa de juros de 2% ao mês..
Pagamento original: 50.000,00 (no quarto mês) e 80.000,00 (no oitavo mês)
Proposta de pagamento: 10.000,00 de entrada, 30.000,00 (no sexto mês) e o restante no ultimo mês.
Repare que o saldo a pagar não se altera com a data focal. Em juros compostos a equivalência financeira independe do momento tomado como comparação.
-
26) Juros Simples – Exercício Proposto
Um empréstimo de R$42.000,00 foi tomado por determinado prazo a uma taxa linear de 7% ao mês. Em determinado momento o devedor resgata este empréstimo e contrai outro no valor de R$200.000,00 pagando 5% de juros simples ao mês por certo prazo. Após de 2 anos de ter contraído o primeiro empréstimo, o devedor liquida sua dívida remanescente. O total dos juros pagos nos dois empréstimos tomados atinge R$180.000,00. Pede-se calcular os prazos referentes a cada um dos empréstimos.
-
25) Juros Simples – Exercício Proposto
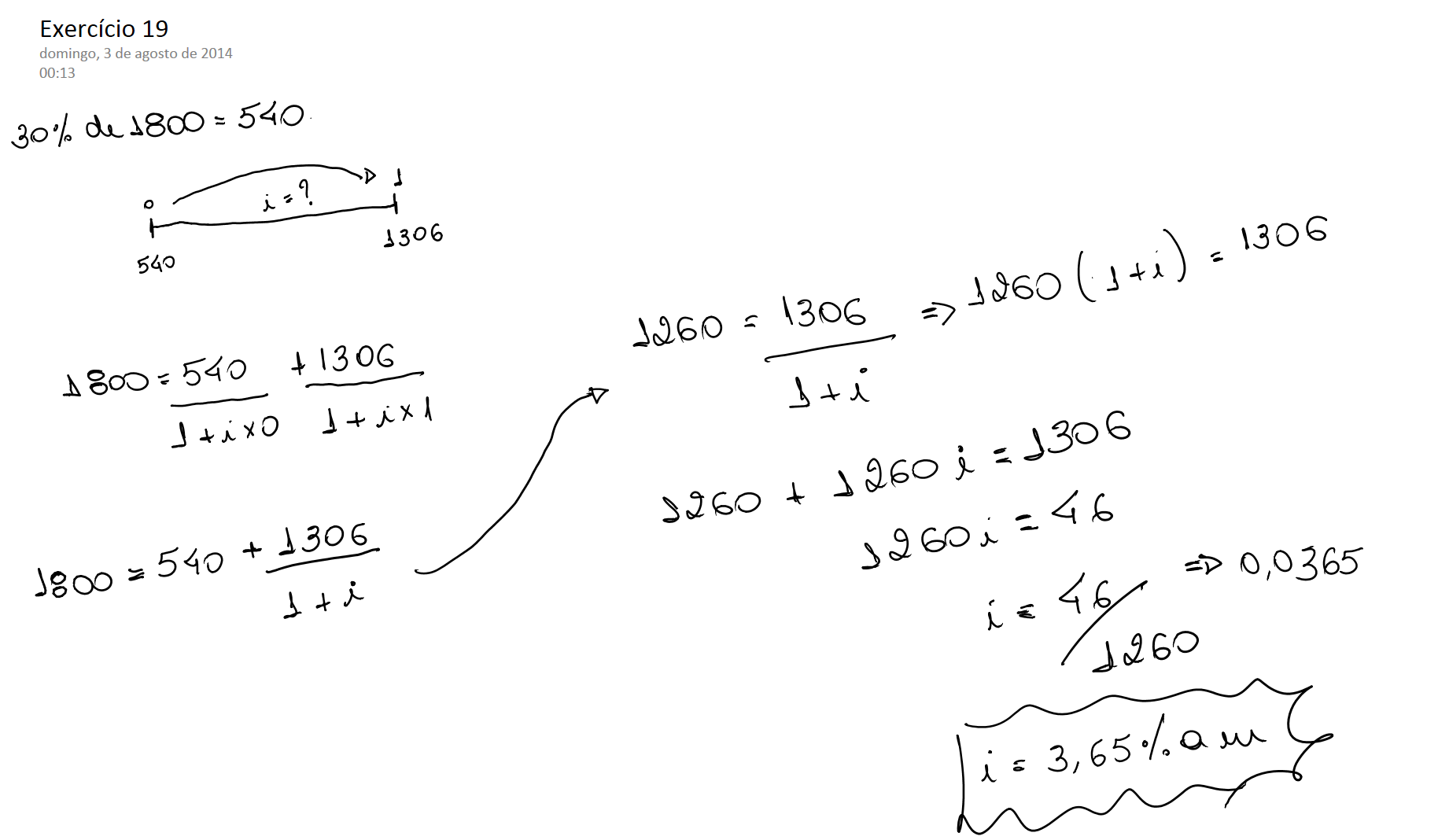
Uma pessoa contrai um empréstimo de R$75.000,00 à taxa linear de 3,3% ao mês. Em determinada data liquida este empréstimo pelo montante de R$92.325,00 e contrai nova dívida no valor de R$40.000,00 pagando uma taxa de juros simples mais baixa. Este último empréstimo é resgatado 10 mêses depois pelo montante de R$49.600,00.
Pede-se calcular:
A) o prazo do primeiro empréstimo e o valor dos juros pagos;
B) a taxa simples de juros mensal e anual cobrada no segundo empréstimo.
-
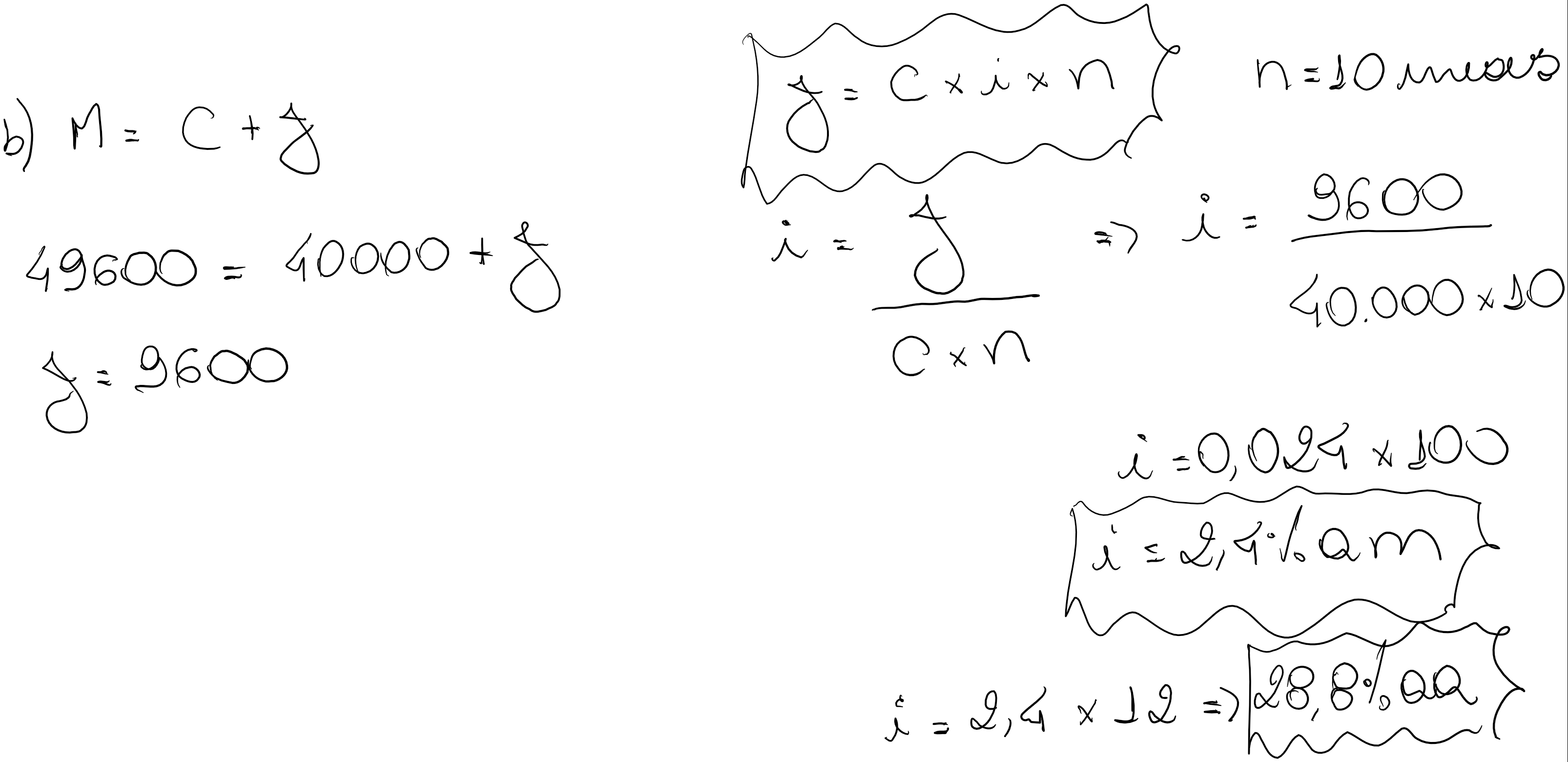
24) Juros Simples – Exercício Proposto
Um poupador com um certo volume de capital deseja diversificar suas aplicações no Mercado financeiro. Para tanto, aplica 60% do capital numa alternativa de investimento que paga 34,2% ao ano de juros simples pelo prazo de 60 Dias.
A outra parte é invertida numa conta de poupança por 30 Dias, sendo remunerada pela taxa linear de 3,1% ao mês. O total dos rendimentos auferidos pelo aplicador atinge R$ 1.562,40. Pede-se calcular o valor de todo o capital investido.
-
23) Juros Simples – Exercício Proposto
Uma pessoa tem uma dívida composta dos seguintes pagamentos:
- R$22.000,00 de hoje a 2 meses;
- R$57.000,00 de hoje a 5 meses
- R$90.000,00 de home a 7 meses
Deseja trocar estas obrigações equivalentemente por dois pagamentos iguais, vencíveis o primeiro ao final do 6 (sexto) mês e o Segundo no 8 (oitavo) mês. Sendo de 3,7% ao mês de juros simples, calcular o valor destes pagamentos admitindo-se as seguintes datas de comparação:
A) Hoje
B) no vencimento do primeiro pagamento proposto
C) no vencimento do Segundo pagamento proposto
-
21) Juros Simples – Exercício Proposto
Um negociante tem as seguintes obrigações de pagamento com um banco:
- R$ 18.000,00 vencíveis em 37 Dias;
- R$ 42.000,00 vencíveis em 83 Dias;
- R$ 100.000,00 vencíveis em 114 Dias;
Com problemas de caixa nestas datas deseja substituir este fluxo de pagamentos pelo seguinte esquema:
- R$20.000,00 em 60 Dias;
- R$50.000,00 em 100 Dias;
- Restante em 150 Dias;
Sendo de 3,2% ao mês a taxa de juros simples adotada pelo banco nestas operações, pede-se calcular o valor do pagamento remanescente adotando com data focal o momento atual.
-
20) Juros Simples – Exercício Proposto
Uma dívida é composta de três pagamentos no valor de R$2800,00, R$4200,00 e R$7000,00, vencíveis em 60, 90 e 150 dias, respectivamente. Sabe-se ainda que a taxa de juros simples de mercado é de 4,5% ao mês. Determinar o valor da dívida se o devedor liquidar os pagamentos:
A) hoje;
B) daqui a 7 meses
-
19) Juros Simples – Exercício Proposto
Uma TV em cores é vendida nas seguintes condições:
- Preço a Vista : R$ 1.800,00
- Condições a prazo: 30% de entrada e R$1.306,00 em 30 dias.
Determinar a taxa de juros simples cobrada na venda a prazo.
-
18) Juros Simples – Exercício Proposto
Uma aplicação de R$15.000,00 é efetuada pelo prazo de 3 meses à taxa de juros simples de 26% ao ano. Que outra quantia deve ser aplicada por 2 meses à taxa linear de 18% ao ano para se obter o mesmo rendimento financeiro?
-
17 ) Montante e Capital – Exercício Proposto
O valor de resgate de um título é 140% maior que o valor da aplicação. Sendo de 30% ao ano a taxa de juros simples, pede-se calcular o prazo da aplicação.
-
16) Montante e Capital – Exercício Proposto
Em quanto tempo triplica um capital que cresce à taxa de 21% ao semestre?
-
15 ) Montante e Capital – Exercício Proposto
Em quanto tempo duplica um capital aplicado à taxa simples de 8% ao ano?
-
14 ) Montante e Capital – Exercício Proposto
Em quanto tempo um capital de R$4.000,00 aplicado a 29,3% ao ano pelo regime linear renderá R$1.940,00?
-
13) Juros Simples – Exercício Proposto
Uma mercadoria é oferecida num magazine por R$130,00 a vista, ou nas seguintes condições: 20% de entrada e um pagamento de R$106,90 em 30 dias. Calcular a taxa linear mensal de juros que está sendo cobrada.
-
12) Juros Simples – Exercício Proposto
Se o valor atual de um título é igual 4/5 de seu valor nominal e o prazo de aplicação for de
15 meses, qual é a taxa de juros simples considerada?
-
11) Juros Simples – Exercício Proposto
Um empréstimo de R$ 3.480,00 foi resgatado 5 meses depois pelo valor de R$3.949,80. Calcular a taxa de juros simples em bases anuais e mensais desta operação.
-
10) Juros Simples – Exercício Proposto
O montante de um capital de R$ 6.600,00 ao final de 7 meses é determinado adicionando-se R$.1090,32 de juros. Calcular a taxa linear mensal e anual utilizada.
-
9) Juros Simples – Exercício Proposto
Uma nota promissória de valor nominal R$ 140.000 é resgatada dois menos antes de seu vencimento. Qual é o valor pago no resgate, sabendo que a taxa de juros simples é de 1,9% ao mês?
-
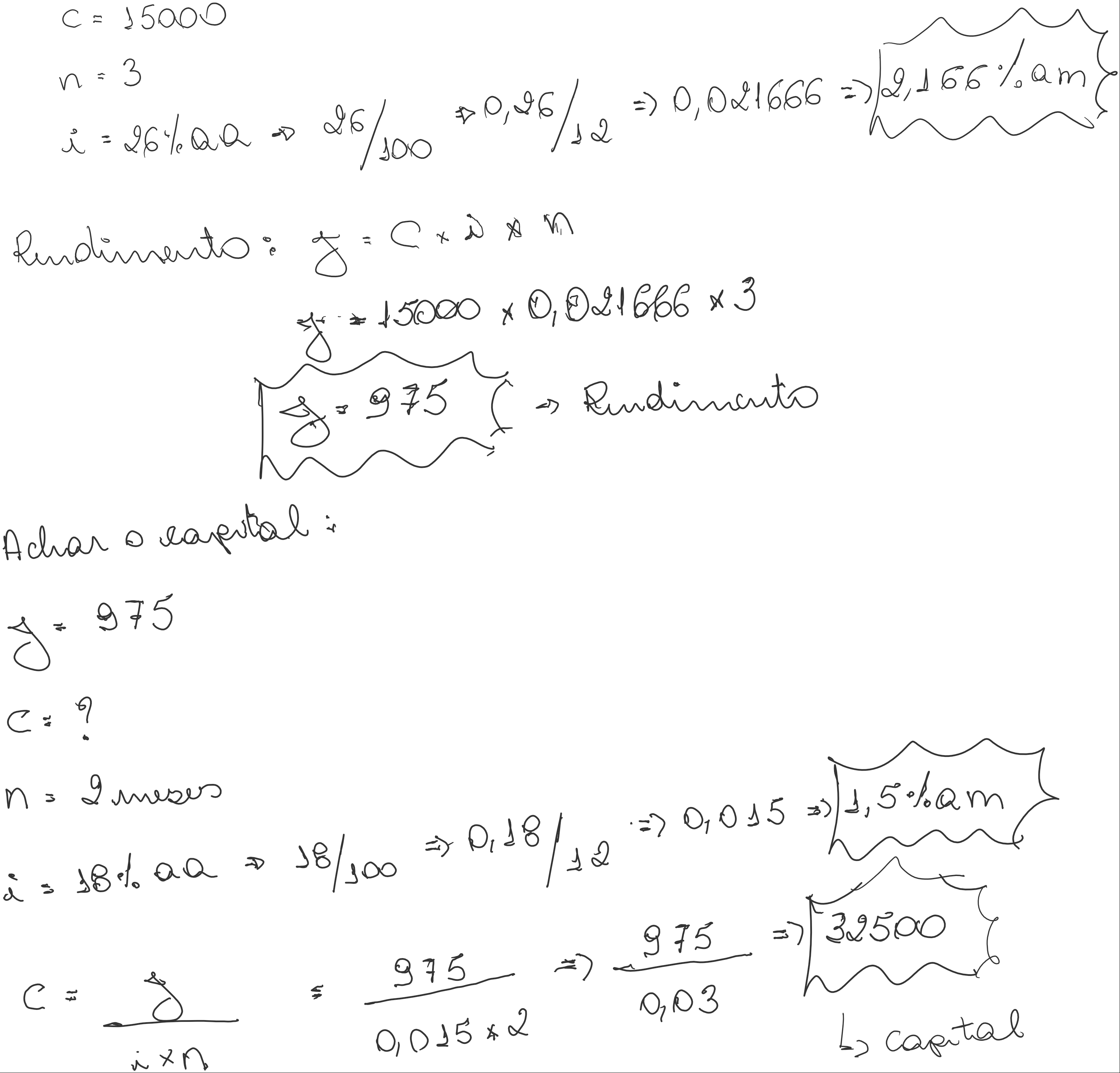
8) Juros Simples – Exercício Proposto
Uma pessoa aplicou R$12.000,00 numa instituição financeira resgatando após 7 meses, o montante de R$13.008,00. Qual a taxa de juros equivalente linear mensal que o aplicador recebeu?
-
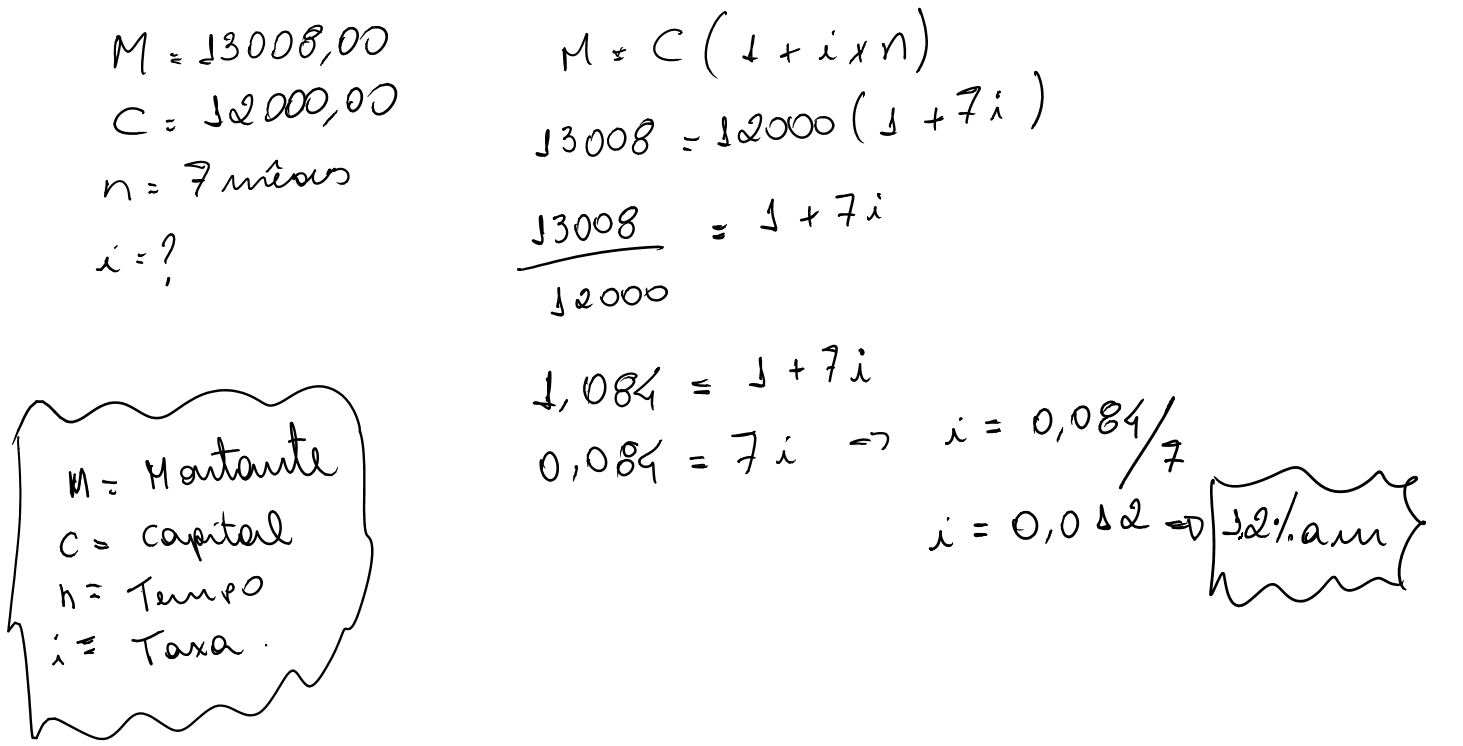
Exercícios Propostos – Taxas
1) Calcular a taxa mensal proporcional de juros de :
a) 14,4% ao ano;
b) 6,8% ao quadrimestre;
c) 11,4% ao semestre;
d) 110,4% ao ano;
e) 54,72% ao biênio;
2) Calcular a taxa trimestral proporcional a juros de:
a) 120% ao ano;
b) 3,2% ao quadrimestre;
c) 1,5% ao mês;
3) Determinar a taxa de juros simples anual proporcional às seguintes taxas:
a) 2,5% ao mês;
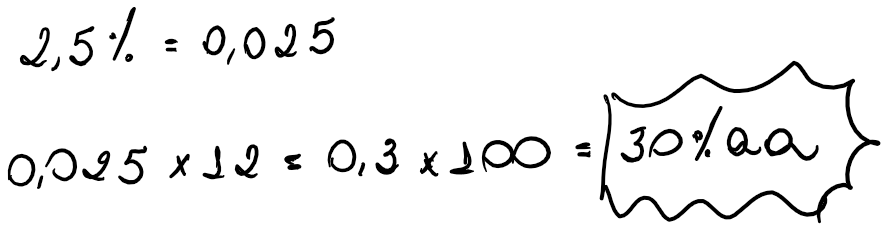
b) 56% ao quadrimestre;
c) 12,5% para 5 meses;
4) Calcular o montante de R$ 85.000,00 aplicado por:
a) 7 meses à taxa linear de 2,5% ao mês;
Utilizando a fórmula
Pode-se também usar a fórmula de montante:
b) 9 meses à taxa linear de 11,6% ao semestre;
9/6 = 1,5 semestre
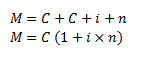
c) 1 ano e 5 meses à taxa linear de 21% ao ano
1 ano e 5 meses = 17 meses.
i=21/12=1,75% am
-
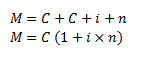
Juro Exato e Juro Comercial – Juros Simples versus Juros Compostos
É comum nas operações de curto prazo, onde predominam as aplicações com taxas referenciais em juros simples e compostos, ter-se o prazo definido em número dias. Nestes casos, o número de dias pode ser calculado de duas maneiras:
a) Pelo tempo exato, utilizando -se efetivamente o calendário do ano civil (365 dias). O Juro apurado desta maneira denomina-se juro exato.
b) pelo ano comercial, o qual admite o mês com 30 dias e o ano com 360 dias. Tem-se, por este critério, a apuração do denominado juro comercial ou ordinário.
Por exempo, 12% ao ano equivale no regime de juros simples a taxa diária seria de :
a) Juro Exato:
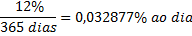
b) Juro Comercial:
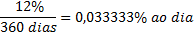
Por exempo, 12% ao ano equivale no regime de juros compostos a taxa diária seria de :
a) Juro Exato:
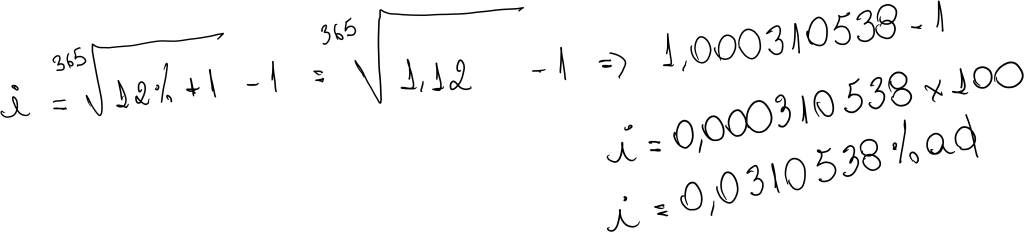
b) Juro Comercial:
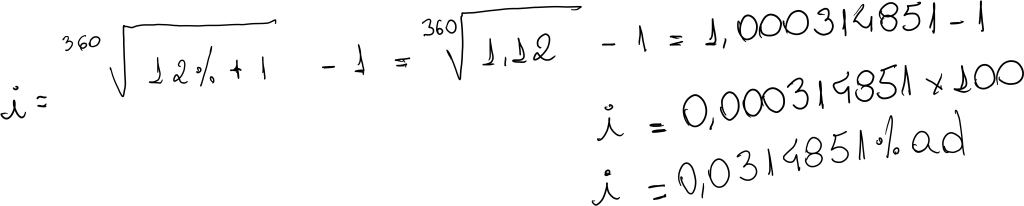
Eu te ajudei? Faça uma doação única para ajudar no meu trabalho.
Escolha um valor
R$5,00R$10,00R$15,00Ou insira uma quantia personalizada
R$
Obrigado pela sua contribuição.
Faça uma doação -
Taxa Proporcional e Taxa Equivalente – Juros Simples
No regime de juros simples, diante de sua própria natureza linear, esta transformação é processada pela denominada taxa proporcional de juros também denominada de taxa linear ou nominal. Esta taxa proporcional é obtida da divisão entre a taxa de juros considerada na operação e o número de vezes em que ocorrerão os juros (quantidade de períodos de capitalização).
Por exemplo: Para taxa de juros de 19% ao ano , se a capitalização for definida mensalmente (ocorrerão 12 vezes juros no período de um ano), o percentual de juros que incidirá sobre o capital a cada mês será:
As taxas de juros simples se dizem equivalente quando, aplicadas a um mesmo capital e pelo mesmo intervalo de tempo, produzem o mesmo volume linear de juros.
Por exemplo, em juros simples, um capital de R$500.000,00, se aplicado a 2,5% ao mês ou 15% ao semestre pelo prazo de um ano, produz o mesmo montante linear de juros. Isto é:
-
Montante e Capital – Juros Simples
Um determinado capital, quando aplicado a uma taxa periódica de juro por determinado tempo, produz um valor acumulado denominado de montante, e identificado em juros simples por M. Em outras palavras, o montante é constituído do capital mais o valor acumulado dos juros, isto é:
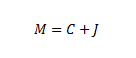
No entanto, sabe-se que:Substituindo esta expressão básica na fórmula do montante supra, e colocando-se C em evidência:
Evidentemente, o valor de C desta fórmula pode ser obtido através de simples transformação algébrica:
A expressão (1 + i x n) é definida como fator de capitalização (ou de valor futuro – FCS) dos juros simples. Ao multiplicar um capital por este valor, corrige-se o seu valor para uma data futura, determinando o montante. O Inverso, ou seja, 1/(1 + i x n) é denominado de fator de atualização (ou de valor presente – FAS). Ao se aplicar o fator sobre um valor expresso em uma data futura, apura-se o seu equivalente numa data atual.
-
Fórmulas de Juros Simples
O valor dos Juros é calculado a partir da seguinte expressão:
onde:
j =valor dos juros expresso em unidades monetárias;
C =capital. É o valor (em $) representativo de determinado momento;
i =taxa de juros, expressa em sua forma unitária;
n=prazo.
Esta fórmula é básica tanto para o cálculo dos juros como dos outros valores financeiros mediante simples dedução algébrica.
Math Financeira 
